�������ȗ��R�ɂ�鏑�����݂̍폜�ɂ��āF �����p�V �Ƃ݂������:�ʔ������w�̖�肨�����ā`�� 40��� ->�摜>17��
����A�摜���o �b�b
���̌f����
�ގ��X��
�f���ꗗ �l�C�X�� ����l�C��
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1640443648/ �q���g�F http ://xxxx.5chb .net/xxxx �̂悤��b �����邾���ł����ŃX���ۑ��A�{���ł��܂��B
�ʔ������w�̖����Љ�ĉ��������X���ł�
����X���ł͂���܂���
�o��҂�������m��Ȃ����͂��T����������
���v�w�Ȃǂ̓X���Ⴂ�A���w�ȊO�̘b��͘_�O�ł�
�r�炵�A����̓X���[����
�O�X��
�ʔ�����肨�����ā`�� 39���
http://2chb.net/r/math/1633923732 �ߋ����O(1-16���)
http://www3.tokai.or.jp/meta/gokudo-/omoshi-log/ �܂Ƃ�wiki
http://w.atwiki.jp/omoshiro2ch/ �ߋ��X��
�ߋ��X�� (����)
�������Ă�ƌ����Ă����Ȃ���K����2���Ԃ����Ă��Ȃ�����
�X���^�C�͑O�X���Ō������悤�ɁA�^�C�g���ɐ��w����ꂳ���Ă������
>>1 �� �e���v������������
�ł͂�������
���� f:R��R �ł����ĔC�ӂ̎��� x,y �ɂ���
f(x-y) = f(x)f(y) + sinx*siny
�������̂�S�ċ��߂�
f(��/2) = f(��/2)f(0) (��x), f(0) = f(��/2)^2+1
>>6 f(x)��萔���Ƃ���� sinx * siny ���萔�ɂȂ�̂Ŗ���
f(x) = f(x)f(0) �Ȃ̂� f(0) = 1
f(x)^2 = f(x - x) - sin^2 x
= 1 - sin^2 x
= cos^2 x
-cosx �͕s�K�Ȃ̂� f(x) = cosx
�ޑ���ǂ��B
�ȉ��̏��������Ƃ���f: R -> R, g: R -> R�̐����ɂ��Ē��ׂ�
1. f(x - y) = f(x)f(y) + g(x)g(y)
2. ��s > 0 s.t. (f(s) = 1 ���� ��x �� [0, s] g(x) >= 0)
>>9 �����A����ȕ��@���c�����ł�
>>10 �����ɂ� f(x)=|cosx| ���̉\�����r������K�v���邩�疞�_�͏o���ɂ������ǁA
�܂������o�Ă邵�C�����ʓ|����Ȃ����낤����OK���ȁc
���Ȃ݂Ɏ����� f(0)=1, f(x)^2=cos^2 x, f������ł��邱�Ƃ܂ŏo���Ƃ����
f(x) = f(x/2-(-x/2)) = cos^2(x/2)-sin^2(x/2) = cosx
�Ƃ���̂�z�肵�Ă܂���
�^��w�̓������
�X�y�[�X������������������
z=rcis(��),w=scis(��),f(z)=r'cis(��'),w='scis(��')
>>12 (1) w��z �Ƃ���bf(z)�b^2���bz�b^2�ƂȂ�̂ŁA�bf(z)�b���bz�b�ł���B
���Ɂbz�b��1�̂Ƃ��A�bf(z)�b��1 �ł���B
(2) a,b��C �ɑ��āba�{b�b^2���ba�b^2�{�bb�b^2�{2Re(a \bar{b}) �ł���A
�E�ӂɂ� Re(a\bar{b}) �Ƃ��������o�����Ă���B���̍��𗘗p����ƁAz,w��C �� r��R �ɑ���
�bf(z�{w)�|f(z)�|f(w)�b^2 �� �c(�n���ɑS�ēW�J)�c �� 0,
�bf(rz)�|rf(z)�b^2 �� �c(�n���ɑS�ēW�J)�c �� 0
�������āA(a),(b)�����藧�B
(3) x,y��R �ɑ��� f(x�{iy)��f(x)�{f(iy)��xf(1)�{yf(i) �Ȃ̂ŁA
f(1)��f(i)�̒l���ڂ�������悢�B
f(1�{i)��f(1)�{f(i) �Ȃ̂ŁA�bf(1)�{f(i)�b���bf(1�{i)�b���b1�{i�b����2 �ł���B
�܂��A�bf(1)�b��1���bf(i)�b�Ȃ̂ŁAf(1)��e^{ia}, f(i)��e^{ib}, a,b��R �ƕ\����B
����āA�be^{ia}�{e^{ib}�b����2 �ł���B���ӂ�2�悷��ƁA2�{2Re(e^{i(b�|a)})��2 �Ȃ̂ŁA
Re(e^{i(b�|a)})��0 �ƂȂ�Ae^{i(b�|a)}���}i �ƂȂ�B
e^{i(b�|a)}��i�̂Ƃ��́Ax,y��R �ɑ��� f(x�{iy)��xf(1)�{yf(i)��e^{ia}(x�{iy) �ƂȂ�B
����� f(z)��e^{ia}z (z��C) ���Ӗ�����B
e^{i(b�|a)}���|i�̂Ƃ��́Ax,y��R �ɑ��� f(x�{iy)��xf(1)�{yf(i)��e^{ia}(x�|iy) �ƂȂ�B
����� f(z)��e^{ia} \bar{z} (z��C) ���Ӗ�����B
>>12 ����͗U���������āi3�j��P�Ƃʼn�������i1�j�i2�j�͎������
����N���Ă���o�J�̂��߂ɂ킴�킴�X���^�C�ɐ��w�����Ȃ���Ȃ��Ƃ�
����ɃX���^�C��ς���Ȃ�
>>17 �ǂ����Ō���(3)�ڎ�����@
{ w f(z)�|z f(w) } { w‾ f(z)�|z‾ f(w) } = 0
������
����Ȃ�v������Ȃ���
��Ƃ肪�n�܂�O�̐���Ȃ�
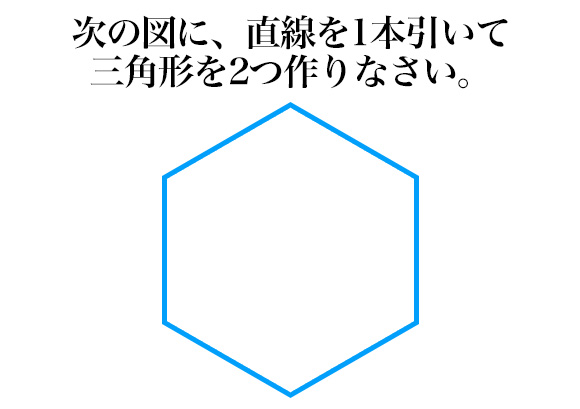
���̏������������ʏ�̐}�`�͉����H
��������
>>6 ����ʉ��ł����B
f,g�FR �� R �͎ʑ��ŁAg(0)��0 ���� f(x�|y)��f(x)f(y)�{g(x)g(y) (��x,y��R) �Ƃ���B
���̂Ƃ��Af(x)��g(x)��0 (��x��R) �܂��� f(x)��1�|2g(x/2)^2 (��x��R) �ł��邱�Ƃ������B
>>23 ����ǂ��납[0, 2��]�̉��Z�̓_��f(x) = cos(x)�ƂȂ邱�Ƃ��ؖ��ł���
>>24-25 ����͕K���������藧���Ȃ��Bf(x) �� cos(3x), g(x) �� sin(3x) �̂Ƃ��A
f,g�FR �� R, g(0)��0, f(x�|y)��f(x)f(y)�{g(x)g(y) (��x,y��R)
�����藧���Ƃ��m���߂��邪�A
f(x) �� cos(x) �ƂȂ� x �� [0,2��] �͈̔͂ɗL�������Ȃ��B
>>23 ��������ŔC�ӂ�x,y�ɂ��� g(x+y) = f(x)g(y) + g(x)f(y) ���o�����
���Ƃ� F(x)=f(x)+ig(x) �ƒu���Ă��ɂ傲�ɂ債����F�X��������
����͐���������Ȃ����ǁA�L�`�̐��w�̖��Ȃ̂��H
(1) �T�C�R����100�U�����Ƃ��̖ڂ̘a��100�ł���m�������߂�B
>>16 ��ABC�̓��S��I�AAI��I�ɂ����Ē������钼����AB,AC�̌�_��D,E�Ƃ���
BD=2,CE=3�ł���Ƃ�DE�����߂�
����ς�X���^�C�ς������x���ᖳ�ʂ�������
�X���^�C�����̍r�炵�͉^�c�ɒʕ�����������
((x))��x�̏��������Ƃ���
>>27 �̎w�E�����ƂɁA�X�Ȃ��ʉ��B
f,g�FR �� R �͎ʑ��ŁAg(0)��0 ���� f(x�|y)��f(x)f(y)�{g(x)g(y) (��x,y��R) �Ƃ���B
���̂Ƃ��A����(i),(ii)�̂��������ꂩ�����藧���Ƃ������B
(i) f(x)��g(x)��0 (��x��R) �ł���B
(ii) ����ʑ� �ƁFR �� R �����݂��āA��(0)��Z, ��(x�{y)�|��(x)�|��(y)��Z (��x,y��R),
f(x) �� cos(2��(x)), g(x) �� sin(2��(x)) (��x��R) �ł���B
�܂��A(ii) �����藧�ꍇ�Af(x)��1�|2g(x/2)^2 (��x��R) �����藧���Ƃ������B
>>33 ��[k=1,N]��[1/(k+1),1/k](1/x-k)dx
=log(N+1) - ��[k=1,N]1/(k+1)
��1-��
�T�C�R����n��(n�͋���)�����ďo���ڂ̘a�����Ғl�ɂȂ�m����
���Ғl�Ƃ������̂͌���������������Ǝv���B
�L�Ӑ����Ƃ��댯�����ƂT���ȉ����ƋH�Ȍ��ۂƔ��f����B
����c�t���ŁA����ŗV��ł���A,B,C,D �����ŗV��ł���E,F,G�̂V�l�̒��ɁA
>>38 �A���^���Ғl���킩���ĂȂ��Ȃ�o�Ă��Ă����H
���w���ď����Ă�̂ɘ_���p�Y�����o����
>>29 (1) �T�C�R����100�U�����Ƃ��̖ڂ̘a��100�ł���m����1/6^100
(2)�T�C�R����100�U�����Ƃ��̖ڂ̘a��101�ł���m����100/6^100=25/(3^2�E6^98)=25/(9�E6^98)
(3)�T�C�R����100�U�����Ƃ��̖ڂ̘a��102�ł���m����(100+9900)/6^100=(2^2�E5^2)/(2^100�E3^100)=25/(2^98�E3^100)
(3)�T�C�R����100�U�����Ƃ��̖ڂ̘a�����Ғl350�ł���m����365�ł���m�����͍����B
�O
>>43 >>40 B��E�͋t�オ�肪�ł����Ȃ����Ȃ��H
�搶�̋C�����I�ɁB
>>40 �����ҁFBD
�t�オ��\�FEF or EG
3���̐_�lA�AB�AC�́A���ꂼ��N�����^�_�A�U�_�A���_�ł��B�^�_�͕K���^���̓������A�U�_�͕K���R�̓����������܂����A���_���^�����邩�R���邩�͊��S�Ƀ����_���ł��B���Ȃ���3�̃C�G�X���m�[���œ����鎿������āAA�AB�AC�̐��́i�^�_���U�_�����_�j�����߂Ă��������B1�̎���ɂ�1���̐_�l���������Ă���܂���i������Ŏ����A�AB�AC�̎w��͉\�j�B�_�l�͎������̌��t�𗝉����܂����A�ԓ��͎������̌��t�ł͂Ȃ��A�_�̌��t�uDa�v�ƁuJa�v�ŕԂ��܂��BDa��Ja�̂ǂ��炪�C�G�X�łǂ��炪�m�[���Ӗ����邩�͕�����܂���B
����ς�X���^�C�ς������x���ᖳ�ʂ�������
>>48 ���������ǂȂ�ł���Ȃɓ{���H
�����Ƃ������w�Ɩ�肾�Ǝv�����ǁH
�����A���R�[���Ƃ��A���G���܂Ƃ�������������p��ł���B
>>30 ���f���ʏ�ɍ�}
�v�������
> abs(D-E)
[1] 4.898979
���܂�
> abs(A-D)
[1] 2.830646
> abs(A-I)
[1] 1.418647
> abs(A-E)
[1] 2.830646
> abs(B-C)
[1] 9.239314
>>46 �_�ǂ����͂��݂��̐��̂�m���Ă���Ƃ����O��ł��傤���H
�T�C�R����n��(n�͋���)�����ďo���ڂ̘a�����Ғl�ɂȂ�m����
>>53 �����\��ꂽ���ɂȂ�ł��܂ł��Ŏ������H
���������̂����f�Ȃ�
�S�O�X���ŃA�z�ɂȂ����ꂽ���
>>43 ������������������������
�a��350�ɂȂ�������
> mean(y==350)
[1] 0.0232915
�a��365�ɂȂ�������
> mean(y==365)
[1] 0.0159091
>>55 �܂��́A�����ōl����������
>>58 �����ōl����̂͏���ɂ������
����������ɏ�������݂�Ȗ��f�����
�ꐶ�������w�̕����āA���͂��āA����Ȃ�ɖʔ������撣���č���ē������p�ӂ��āA���ꂪ�����������傤���Ȃ��A��������Ȃ����X�ɂǂ�ǂ���Č����Ă鎞�̋C�����킩��H
�������ǂꂾ�����w�I�ɂȂ�̈Ӗ����Ȃ����f�Ȃ����̃��X��\�葱���Ă邩�킩���́H
���ɂ͂������ʔ������삪����ł�̂킩��H
�݂�Ȃ�����ǂꂾ���撣���ď������Ă�̂��z���ł���́H
�`���̃X���̊F����ց`
���݁A���Ӗ��ȃv���O�������������ވ����ȍr�炵���풓���Ă��܂�
�ʏ̢�v���O�����L�`�K�C���Q���v���O������������͈�ÁE��Ҕɂ���A�r�A�]����҂ƌĂ�Ă���r�炵�ł�
http://2chb.net/r/hosp/1607687111/ ���wI�̎O�p��̖��⒆�w���w�̕��ʐ}�`�̖��ł�����v�Z�ł͉�������
�킴�킴�v���O�����ʼn����悤�Ȑl���ł�
���z�̊��Ғlnp����m��Ȃ����x���ł�
���Ȃ��x���̐��w�̖����ǂ����o�肵�ă}�E���g�����ɗ��܂�
���l�^����D���ł�
>>41 ���҂Ƃ������{��ɂ�positive�Ȋܒ~������B���҂����l�ԂƂ����Ɩv�������҂���Ă͂��Ȃ��Ǝv���B
hot water�Ɉ�a���͂Ȃ����M�����Ƃ����͈̂�a�����o����B
expcted loss�����ґ����Ɩ͔̂M�����Ɠ�����a����������B
�����̂������ł��Ȃ��C�̓łȓ��̂悤�ł���B
>>59 �ʔ����ƍl�����l���A�T�C�R����100�U�����Ƃ��̖ڂ̘a�Ƃ��_���p�Y���Ƀ��X���Ă�Ȃ��́H
>30�̖����Đ��w�I�ɉ����Ӗ�������́H
���͉����̂��ʔ��������}���Čv�������B
�܂��A�v���O�����ŕ������̐��l�����o���č��W���v�Z���Ē������v������Ƃ����̂���������������B
>>57 ���N���N���҂��Ă����̂ɁA���҂ǂ���i���Ғl�ǂ���j�ɂȂ�p�x���Q���Ƃ͊��ҊO��Ƒ̊��ł����B
�E����[
>>41 ���҂Ƃ������{��ɂ�positive�Ȋܒ~������B���҂����l�ԂƂ����Ɩv�������҂���Ă͂��Ȃ��Ǝv���B
hot water�Ɉ�a���͂Ȃ����M�����Ƃ����͈̂�a�����o����B
expected loss�����ґ����Ɩ͔̂M�����Ɠ�����a����������B
���������̂������ł��Ȃ��C�̓łȓ��̂悤�ł���B
>>63-65 ��p�̃X����������̂ŁA
����A�����������͈ȉ��̃X���ɏ�������ł��������B
���l��̖͂����������ރX��
http://2chb.net/r/math/1640641452/ ����ɐ��l��͂𒆐S�Ƃ�������Љ�ĉ��������X���ł�
��
�����w�I�Ȍ����������܂肻���ɂȂ��A
���v���O�����E�V�~�����[�V�������ŊT�Z�l���o����Ώ\���A
���Ƃ�����肪���S�ƂȂ�܂�
��
���������A���ʂ̐��w�̖����n�j
>>65 �X���^�C���ǂ߂Ȃ��C�̓łȓ��̂悤�ł���
>>63 ��������������������
���O�����Ő��w�̕������L���Ȃ����H
���w�����Ă邵���l�Ԃ�����ʔ����Ǝv���̂��A�����Q�l�ɂȂ�̂��Ȃ��O�݂����Ȕ\�����̃J�X�ɂ킩��킯�Ȃ����H
�ق��ă������Ƃ�
�\����
����f:R��R�ł����ĔC�ӂ̎���x,y�ɂ���
���p�ꂪ��ʗp���connotation����O���B
>>70 �o�J�̕��͂͂Ђ炪�Ȃ��߂���w
���������߂���C�P�̃e�X�g�œˑR�Ђ炪�Ȃ�������̂��o�J�̓����݂����Ȃ��ƌ����Ă���ww
>>68 ���������̂����������l�|����тƂ���N�Y�l�Ԃ̓T�^�B
>>73 ����u�[������
�S���A���^�̂��Ƃ��悻��
���������l�|�~�������������e���������
���w�X���ɂ͂��������̂������ˁB
���l��̖͂����������ރX��
http://2chb.net/r/math/1640641452/5 5 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2021/12/28(��) 10:53:21.01 ID:V7fjP+Uc
>>1 �悻�ł��
�܂�A�����ł��Ƃ́u�����v����Ȃ�����
���āA�x���`�^�C�����I������̂Ő��`���ē��y�ɂƂ肩���낤�B
>>75 ���̐l�̓A���^�̌����Ɏ����Ă邾�����ƋC�Â��Ȃ��̂������
>>70 �W�Ȃ��G�k�̕p�x���߂��Ă�Ǝv������G�k�͂������ł���Ă�
�G�k�͂����ɏ����I�y�U�P�z
http://2chb.net/r/math/1637315946/ ����
>>75 ���̖�肪���v�X��
http://2chb.net/r/math/1640641452/5 �̕����K���Ă��鎖���͕ς��Ȃ����獡��͂������ɓ��e���邱��
���̖�肪�ʔ����Ȃ��i����ɂ������j�Ɗ����Ă���l���吨�������
���߂ăR�e���Ă����������q�ł���悤�ɂ��邮�炢�̔z���͂��Ă�
�A����f:R��R���āA
>>79 �������Ă��̂�
���̏ꍇ��(�E�́E)���Ԃł��肢���܂�
>>69 ���� z ��C�ӂɎ��Ax��z�|��/2, y����/2 �Ƃ��āA
f(z)��f(z�|��/2)cos(��/2)�{f(��/2)cos(z�|��/2)��f(��/2)sin(z)
���ꂪ�C�ӂ� z �Ō�����̂ŁA���ǁA���� �Ɂ�R �ɑ���
f(x)����sin(x) (��x��R) �ƂȂ�B�t�ɁA���̂悤�ɕ\���� f �͗^�������B
>>78 �ł���
�W��Fn��
Fn = { x > 0 ; ��m��n |f(nx)|���� }
�Œ�߂�
����ɂ��(0,��) = ��Fn �ł���
�x�[���̃J�e�S���[�藝�ɂ�菭�Ȃ��Ƃ����Fn�͓��_�������Ȃ���Ȃ�Ȃ�
(a,b)��Fn�Ƃ���
n0>n��1+1/n0<b/a�ƑI�ׂΔC�ӂ�m��n0�ɑ���(m+1)a<mb�ł���
����
��[m��n0](ma,mb) = (n0a,��)�ł���
�����x>n0a�̂Ƃ�m>n0��y��(a,b)��x=my�Ǝ��邪���̎�|f(x)|=|f(my)|���Âł���
������
>>83 �f���炵���ł� �������吳��
�܂������W����F_n�������u���ăx�[���̔��e�藝���g���̂��~�\�ł���
���l�^
���w�ڂ�������āI�I�I�I�I
http://2chb.net/r/news4vip/1640629371/ ����
>>1 �͈�T�Ԋ|���ĉ����o���Ȃ������ƌ����Ă����̂ɁA�����������Ԃʼn�����Ƃ͂������ł���
>>85 �������ȑ哹��K�v�Ȃ��
������
>>87 ����͂ǂ��Ȃ낤
���ƌl�I�ɋC�ɂȂ�̂�
�A�������ۂ��Ȃ�������
>>78 �̔��Ⴊ�o����̂��H
�Ƃ������Ƃł���
>>82 �����I�V���v���ł�����
>>88 �A������Ȃ����̔���͗Ⴆ��
f(x)=1 (���鐮��m�ɂ��� x=e^m ������),
f(x)=0 (����ȊO)
�������Ȃ�����
�X�� x>0 �ɂ��� f(xn)>0 �������̐���n�͍��X�������
lim(n����) f(xn)=0 �͐��藧���A���
lim(x����) f(x)=0 �͐��藧���Ȃ�
�A�������Ȃ��������ł����Ⴀ��܂�����
>>88 �������������
�����
�������Ǝア�Ƃ�����̏ؖ��������Ă�����ׂ����Ƃ����v�Ă�
>>89 >>90 ������ ���肪�Ƃ��������܂�
���[�Ȃ�قǐ������݂ł��邱�Ƃ𗘗p����
�u������n��f(nx)��0�Ƃ͂Ȃ�Ȃ��v���Ƃ��������̂� �f���炵��
�N�\�[��������������p�b�Ǝv�������ׂ�悤�ɂȂ肽����
����
1,3,8,21,55,144,377,�c
(3�{���đO�̐���������������̐�)
��
����
1,3,10,33,109,360,1189,�c
(3�{���đO�̐��𑫂���������̐�)
�̕��ς�
>>84 �̐���
1,3,9,27,82,252,783,�c
�ɂȂ�
9���ڂ����߂��7777
�f���̗L���W���ő������ς�2022�ł�����̂̌����̍ő�l�����߂�
��ʂ̂��Ȃ�100�̋ʂ���ʂ̂��Ȃ�5�̔��ɓ����B
���N��100���~��1���~�P�ʂ�6�l�ŕ����镪�����͉��ʂ肠�邩�H
119 �P�R�Q�l�ڂ̑f������[sage] 2021/12/31(��) 10:50:19.35 ID:QNczF9a7
���낤 �u����ӊO�ƒm��Ȃ�����������ł�����
���� a_n = ��_(k=1,n) sin(sin(k)) �͗L�E�ł��邱�Ƃ�����
a_i,j(1��i,j��n)��
>>105 xi=��iq,yj=��jp�Ƃ����a_pq=0
>>106 ������ sin(sin(x)) ���e�C���[�W�J���Ă��ꂼ��̍���]�����銴��
�����̖������x�Ɋւ��錋�ʂ��g���Ǝv��
>>108 �������A�t�[���G�W�J
�O
>>44 >>102 �f���ŋ����Ȃ̂�2��������i(-�-)
>>110 ������đO��Ƃ���
�u���R���̂����A�����łȂ����̂͊�ł���v
���Ă����̂��K�v����ˁH
������ďؖ�����Ă���́H
��ł������ł��Ȃ��f�������݂���\���͂ǂ��ȂH
���R���́u�����A��A���̂ǂ���ł��Ȃ��v
��3�̏W�c�ɕ�������ƍl���Ă݂悤�B
��������ƁA
�u�f���̂قƂ�ǂ���v�Ƃ����\���͂��������Ȃ��B
>>108 �_����
��搶�������Ă���Ȃ�
sin(sin(x))�̃t�[���G�����W�J�����ł������ĉ�����
>>108 �_����
�~�����̖������x���ォ��̕]�������傱���傱���邾���łǂ��g���������T�b�p���킩��Ȃ�
���������q���g��
>>112 >>113 �t�[���G�W�� sin(sin(x)) = ��_(m=1,��) c_m�sin(mx) �͌����Ȓl�͕K�v����Ȃ��āA
�C�ӂ̒萔 r>0 �ɂ��� c_m=O(m^(-r)) (k����) �ł��邱�Ƃ����ŏ\��
���Ȃ�̖������x���L���ł��邱�Ƃ����g��Ȃ��Ǝv��
�ؖ��̎n�߂�
|a_n| = |��_(k=1,n) sin(sin(k))|
= |��_(k=1,n) ��_(m=1,��) c_m sin(km)|
�� ��_(m=1,��) c_m |��_(k=1,n) sin(km)|
�c�Ƃ���Ȋ����ɂȂ邩��
>>114 ���H
���Ⴀ�t�[���G�����W�J�����C�ӂ̎���2�̊��ł�������Ď��H
�Ƃ������t�[���G�����W�J����
>>104 �̋ؓ��͂킩�����B
sin(sin(x)) = a[1] sin(x) + a[3] sin(3x) + a[5] sin(5x) + ...
���̌W���̓x�b�Z�����̕�����
a[m] = 2*BesselJ[m](1)
�Z�W���̕]��
�x�b�Z�����̐ϕ��\�����
|BesselJ[m](1)|
= (1/2)^m/(���(m+1/2))|��[0,��]cos(cos(x))sin(x)^(2m)dx|
�����/(2^m ��(m+1/2))
�Z���ʋ����̕]��
|��[k=1,n]sin(mk)|
=|sin(mn/2)sin(m(n+1)/2)/sin(m/2)|
��1/|sin(m/2)|
����������
|��[k=1,n]sin(sin(k))|
����[j=0,��] ���/(2^(2j) ��(2j+3/2)|sin(j+1/2)|)
���Ƃ͉~�����̖������x�̕]������j�̘a���L�E�ɂȂ邱�Ƃ������悢�B
>>115 ���₢��Asin(sin(x)) �̏ꍇ��C^���������A
���̕��� ��_[0,2��] sin(sin(x))dx �̒l��0�������
�s�A���Ȋ��Ƃ����Ƃ����͂����Ȃ�
>>114 �̖������x���L���Ƃ����̂�
����萔c>0�����݂��ĔC�ӂ̎��R��p,q�ɑ���
|��-p/q| >1/q^c
����������
�ō����Ă�H
�t�[���G�����W�J������ʂ̊��ɂ��Č����Ă鐫���Ə�̎����������玦����ŊԈႢ�Ȃ��H
���A������
>>117 �����������ƁI
���Ƃ͖������x���g�������肩��
�������l�������l�̂��߂ɕߑ�
�̖������x�̗L��������A1/�̖������x�̗L�����������邱�Ƃɒ��ӁB
���ƁA���� r �Ɉ�ԋ߂����� n ���Ƃ�� |sin(��r)|��2|r-n| �Ƃ����]����������B
�������g��������� A,B>0 �����݂��āA���̐���j�ɂ���
1/|sin(j/2)| �� Aj^B
�����藧���Ƃ���
>>119 ����B�m���Ƃ��Ă�C^�����̃t�[���G�W���̃I�[�_�[�ƁA
�̖������x�̗L���������ő����͂�
>>121 ����A���l���ĂĂ����܂ł͍s����
�������t�[���G�����̕���l^1�ɓ����Ă邩������Е���1/cos(km)��m�ɂ��ėL�E�Ƃ��Ȃ�l^1�~l^����l^1�ɓ����Ă����
������1/cos(km)�̏ォ��]�����ł���
inf { | l ��/2 - km | ; l } �Ƃ���������]�����邱�ƂɂȂ邯�ǖ������x�L�����猾����̂�j���Ƃ���
| ��/2 - km/l | > l^j
�Ƃ����]���������邾����
��������1/cos(km)���ǂ�����ďォ��]�����Ă������������
�t�[���G�����̕���l^1�ȏ�̉����͖]�߂Ȃ���ˁH
>>123 1/|sin(k/2)|�̂��ƁH
>>117 �ŋ�̓I�ɒ��Ă��ꂽ�ʂ�A
�W����l^1�ł���ȏ�Ɏw�����I�Ȍ��������Ă���邩��
1/|sin(k/2)|�𑽍����ŗ}����Ύ������͏\��������Ǝv������
>>124 ����A������
��͂�Œ�ł�sin(sin(x))�̂悤�ȋ̂������łȂ��ƃ_�����
�O��sin���}�N���[�����W�J����
��[u:odd](-1)^((u-1)/2)1/u!(sin(x))^u
��m���̃t�[���G�W�J�̌W���͂��̌W����(sin(mx),(sin(x)^u) (������(,)��L^[-��,��]�̓��ρAsin(mx)�̒�����1�ɂȂ�悤�Ɏ���Ă���)��������u��m�ő������킹�邯��(sin(mx),(sin(x)^u) �̔��U��蕪���u!�̕��������Řa��1/m!��菬�����Ȃ邩�牱���
��[k]sin(km)�������I�ɑ�����̂������肵�Ă�
A��[0,1]^2 �̓{�������ŁA����2�������x�[�O���x�͐��Ƃ���B
>>127 R^2�̃��x�[�O���x���ʂƒu���Ƃ��A��(A)��0 �Ƃ����Ӗ��B
�������������琴����������B
>>129 X = R�~R�~R�~R�̍��W����x1,x2,y1,y2�Ƃ��ĕW��F��{ x1=x2 or y1=y2 }�Ƃ���
F(x1,x2,y1,y2) = | x1-x2||y1-y2|�Ƃ���
��Ԃ̗�In,Jn,Kn,Ln�Ɛ��̐��̗�cn��
��In�~Jn�~Kn�~Ln = X�_F, p����In�~Jn�~Kn�~Ln��F(p)>cn
�ƂƂ��Ă���
���肩�班�Ȃ��Ƃ����n��
��(A�~A�~A�~A �� In�~Jn�~Kn�~Ln) > 0
�ł��邩�炱�̎���[A�~A�~A�~A]f(p)dp > 0�ł���
����ē���A�~A�~A�~A��0�ł͂Ȃ�
f(p)��0�ł���A�~A�~A�~A�̓_p=(x1,x2,y1,y2)���Ƃ���ꂪ��������
>>130 ����(A�~A�~A�~A �� In�~Jn�~Kn�~Ln) > 0
�������������B��������v���ĂȂ��B
A��[0,1]^2 �Ȃ̂ŁAA�~A�~A�~A �� R^8 �ƂȂ邪�A
In,Jn,Kn,Ln �� R �̕�ԂȂ̂ŁAIn�~Jn�~Kn�~Ln �� R^4.
>>129 ��������B�܂�AA��[0,1]^2 �����x�[�O���ȏW���Ƃ��鎞�A
�����قȂ� x1,x2��[0,1] �ƈقȂ� y1,y2��[0,1] �ɂ���
(xi,yj) (i,j=1,2) �̑S�Ă�A�̌��ɂȂ邱�Ƃ��Ȃ��Ȃ�A
A�̃��x�[�O���x��0�ƂȂ邱�Ƃ������B
R^3�̕����W��B�� B' = {(x1,x2,y)��R^3 | (x1,y),(x2,y)��A} �ƒ�߂�B
����̓��x�[�O���x ��(A)^2 ������ A^2��[0,1]^4 �̎ˉe�ł��邩��A
��(A)^2����(B') �����藧�B
�܂��AP={(x1x2,y)��R^3 : x1��x2} �̃��x�[�O���x��0�ł��邩��A
B=B'-P �ƒ�߂�� ��(B)=��(B') �����藧�B
�����ŁA������_ (x1,x2,y),(x1,x2,y')��R^3 ������B�̌��ł���Ƃ���ƁA
B�̒�`��� x1��x2 �ƂȂ邪�A�����A�̉����� y=y' �łȂ���Ȃ�Ȃ��B
����ďW��B�́Ay���i���ӁFy�͑�O�����j�ƕ��s�ȔC�ӂ̒����Ƃ̌�_�͍��X��B
�䂦�� ��(B)=0 �ł��邩�� ��(A)=0.
>>133 ��H�ˉe�̂����肪�����ςȋC������
������ƕۗ�
>>129 �ł���
�e�Ղ�A��I�~I�Ƃ��Ă悢�Ƃ킩��( ������I = [0,1] )
�ex��I�ɑ���Ax={y | (x,y)��A}�Ƃ���
�܂�S = {x | ��(Ax)>0}�͔�Z�ł���
�����łȂ����A' = A�_��[x��S]Ax�Ƃ�����S���Z�Ȃ�A'�����Ń�(A')=��(A)�łȂ���Ȃ�Ȃ��������Fubini�̒藝���
��(A') = ��[x]��({y|(x,y)��A'})dx = 0
�ƂȂ�̂Ŗ�������
���̎�S�̉Z�����W��C�Ɛ��̒萔e>0����(Ax)>e�ƑI�Ԃ��Ƃ��ł���
���̂Ȃ�̓�:S��(0,��)��x����(Ax)�Œ�߂鎞�����ꂩ�̎��R��n�Ń�^(-1)((1/2^n,1/2^(n-1)])����Z�W���ƂȂ�˂Ȃ�Ȃ����炻������Z�����W��C��I��e=1/2^n�Ǝ��悢
���̎�C����قȂ�2�_x,x'����(Ax��Ax')>0�ƂȂ�悤�ɑI�ׂ�
�����łȂ����C�̌���x1,x2,...�ƕ��ׂ�Bxi = Axi �_��[j<i]Axj�ƒ�߂��Bxi�݂͌��ɑf�őS�đ��x��e���傫�������(��Bxi) = ���ƂȂ邪�A�R����Bxi���S��I�̕����W���ł��邱�Ƃɔ�����
�ȏ�ɂ��C����2�_x,x'����(Ax��Ax')>0�ƑI�ׂ邪�A���̎�����Ax��Ax'�͈قȂ�2�_���܂ށ�
>>135 S �͎��ۂɔ�Z�����A���̏ؖ����������������B
�� A' = A�_��[x��S]Ax
Ax �� R �Ȃ̂� ��[x��S]Ax��R �����A����� A��R^2 �Ȃ̂ŁA
A�_��[x��S]Ax �͎����̈قȂ�W���̍�������Ă��ĈӖ��𐬂��Ȃ��悤�Ɍ�����B
����ȊO�̕����͘_�؍��݂ō����Ă�Ǝv���B
�O
>>110 ���R���͊�����R�̂ǂ��炩�ł��B
����2�ȊO�̋����͂��ׂ�2�Ŋ���܂��B
�� �f���ŋ����Ȃ̂�2��������i(-�-)
>>136 ����������������
A'= A�_��[x��S] {(x,y) | y��Ax }
��
�Z�����Ȃ�x��S�ɑ��ā�[x��S] {(x,y) | y��Ax }��
�܂������Ȃ��Ă��ǂ݂̂���[x��S] {(x,y) | y��Ax }�͑��x0�Ȃ���
>>137 ���R��������������̂ǂ��炩�ł������
����Ȃ̖����ɏؖ�����Ă��Ȃ���B
�O>>137 ����Ȃ̂���������݂ɂȂ��łA������1���̓�������B������ȊO�Ɏ��R���͂Ȃ���B �ɂԂ���
>>138 �����B����Ȃ���v�����B�܂��t�������Ă����ƁA
S �����X�Z�Ȃ�A��(Ax)��0 a.e.x��[0,1] �Ȃ̂�
��(A)����[0,1] ��(Ax) dx �� 0 �ƂȂ��Ė����B����� S �͔�Z�B
�c�̕������ړI���ȂƂ͎v���B
�藝
������ƌ_��ȁI�I
>>143 >>139 ���Ă���Ȃɕς��H
�u�g�����������_�v�Ƃ��ŒT����
���ۂɂǂ����̒N�����l�����������B
>>145 ����������
��ʉ������咣�܂ōڂ��Ă��肪�Ƃ��������܂�
������
�ȈՓI�ȑz����Ƃ��āA(cos1��)^2 = 1/(1+tan1��)��Q(tan1��)���A
Q(tan1��)��Q(cos2��)�ŁA
x^2 -2(cos2��)x +1 = 0�̍�����_180�ł��邩��A
[Q(��_180):Q(cos2��)]=2���A
[Q(tan1��):Q]��[Q(cos2��):Q]=��(180)/2=24
����������(tan1��)^20�͖�����
�Ƃ������̂ł���
����Ɉ�ʉ�
>>145 ����(tan1��)^30�Ƃ��͗L�����ɂȂ�\����ے�ł��ĂȂ�
�藝�@3�ȏ�̎��R��n�ɂ����āA���鎩�R��m��(cot(2��/n))^m���L�����ƂȂ�̂�n = 3,4,6,8,12�̂Ƃ��ł���
���@0�łȂ�����a�ɂ����āAI = { m��Z | a^m ��Q }���O�ȊO�̐������܂ނƂ���
���̎�m��I�ɑ����鐳�̐��̍ŏ��l�Ƃ����x^m-a^m��a�̍ŏ��������ł���
(��) ��=exp(2��i/m)�Ƃ���
a�̍ŏ���������x^m-a^m�̈��q�ł��邩��a�̋�������a��^k�ƕ\�������
�����S��{0,1,..,m-1}��{ a��^k | k��S } ��a�̋������S�̂ƂȂ�悤�ɂƂ��
���̎�N(a) = �}a^#S���L�����ƂȂ�(������N:Q(��,a)��Q�̓m�����ʑ�)
����#S��I�ł��邩��m��#S�ł���
������S�̎������疾�炩��#S��m�ł��邩��#S = m�ł���a�͂��傤��m�̋�����������
(�藝�̏ؖ�) I = { m��Z | cot(2��/n))^m��Q }�����R�����܂ނƂ���
�����I�̐��̐��̍ŏ��lm������x^m - cot(2��/n)^m��cot(2��/n)�̍ŏ��������ƂȂ�
����cot(2��/n)exp(2��i/m)��cot(2��/n)�̋������ƂȂ�
�����������Q(cot(2��/n))��Q�̃A�[�x���g��ł������Q�̃K���A�g��ŋ�������鑀��ɂ��ĕ��Ă���
�����cot(2��/n)exp(2��i/m)��Q(cot(2��/n))�̌��łȂ���Ȃ炸�A����ē��Ɏ����łȂ���Ȃ�Ȃ�
�����m=1,2����������Ȃ�
�����[Q(cot(2��i/n)):Q] = 1,2���������ꂸ�O�藝���
n:��A��(n) = 1,2
n��2 ( mod 4 ), ��(n) = 1,2
n��4 ( mod 8 ), ��(n) = 2,4
n��0 ( mod 8 ), ��(n) = 4,8
���K�v�ł���
�R������3�ȏ�̎��R����n = 3,6,4,12,8,16,24�����Ȃ��A�����
cot(2��/3)=-1/��3,
cot(2��/6)=1/��3,
cot(2��/4)=0,
cot(2��/12)=��3,
cot(2��/8)=1,
cot(2��/16)=1+��2,
cot(2��/24)=2+��3
�ł��邩��咣�͐������遠
>>149 ����Ȃ�lj��̈�ʖ�������肪�Ƃ�
�Ȃ�قNJm���əp����ʂ̏ꍇ�ǂ�����̂��l���ĂȂ������ł���
��_m��Q(cot(2��/n))��m=1,2�̂�(����ȏゾ�Ƌ������܂�)���g�原����1,2�̂�
�Ƃ�������͂ƂĂ��������ł���
>>151 �����A���O���撣��� �i�@'�e�ցe)
f:R��R��������\�Ȋ��Ƃ���
�������łȂ����́A�����ׂ������ɓW�J�B
>>154 C^��������Ƃ����āA�����ׂ������ɓW�J�ł���Ƃ͌���܂���
�L���ȗ�ł�����
f(x) = e^(-1/x^2) (x �� 0)
, 0 (x �� 0)
�Ȃ������ł�
>>154 ����Ɍ�����
�Ⴆ�����W�J�o�����Ƃ��Ă��A
>>153 �̏�������A�������ɂ͗L�������ɂȂ邱�Ƃ͎����Ȃ��̂ł͂Ȃ��ł��傤��
�u���x���v��������a���������0�ɂȂ�
���̔����̉�a�Ɉˑ����Ă��܂�
�܂�����a�Ɉˑ���������ɏ�E������Ύ��������ǂ����łȂ����ɂǂ����邩
>>156 �����������
>>154 �ċU�Ȃ�Ȃ����H
����A�K���ɏ������̂ŁA�y���X���[���Ă���B���܂�B
>>158 >>153 ���U�ł͂Ȃ��̂�
�L�������ɓW�J�̑�����
�Ȃ̂͊m���Ȃ��Ƃł�
>>161 >>83 �̂悤�Ƀx�[���̃J�e�S���[�藝���g���܂��I
>>163 �Ƃ肠�����W����
Fn = { x | f^k(x)=0 ��k��n }
�Ƃ��ł����H
�������R�����J��Ԃ������ĂĂ����̑����ɂ��Ȃ�Ȃ��C��
�����ƕʂ̐ݒ�ł����H
���Af^k(x)=0����Ȃ���f^(k)(x)=0
�킩����
>>165 �������I
��ϔ����������肪�Ƃ��������܂�
���̂悤�ɁA�x�[���̃J�e�S���[�藝��
�u�C�ӂ�x��R�ɑ��Ă���n��N�����݂��āA�Ȃz�j�����������v
�݂����Ȗ���́u�C�Ӂv�Ɓu���݁v���Ђ�����Ԃ������Ƃ��A�x�X���ɗ���
�Ƃ������b�ł���
��[�H�����������ł��ĂȂ��̂��ȁc
>>153 ���āw�e x��R �ɑ��Ă��鎩�R�� n �����݂��Af^(n)(x)=0 �����藧�x���ĈӖ��ō����Ă�H
�����w�e x��R �ɑ��Ă��鎩�R�� n �����݂��A�C�ӂ̐��� k��n �ɂ��� f^(k)(x)=0 �����藧�x
���ĈӖ��ŏ����Ă���A�����̓ǂ݈Ⴂ���Ă��ƂŐ\����Ȃ�����
�O�҂̉��߂ō����Ă�Ȃ�A
>>165 �̉� Fn ����
�S�ċ�W���ɂȂ�\�������蓾��̂ł́H
��������ƁA�ǂ��x�ł�����ԍ���intFn�ɓ���Ƃ����̂͐��藧���Ȃ��Ǝv������
>>168 �m���ɂ����ǂ߂��
�ł�����Ȃ�
Fn = { x ; f^(n)(x) = 0 }
�ł��Γ���
>>168 ���݂܂���O�҂�
�u�e x��R �ɑ��Ă��鎩�R�� n �����݂��Af^(n)(x)=0 �����藧�v
�Ƃ����Ӗ��ŏ����Ă��܂���
�Ȃ̂�
>>169 �̒ʂ�F_n�͂�������ׂ��ł�����
>>169 ���[�������Ȃ�ق�
������
>>165 �̂悭�킩��Ȃ����������悤�₭���ȉ����ł������ۂ�
�w����ԍ���intFn�ɓ���x�����߂� ��_n Fn = R �Ƃ���������g���Ă�킯��
��� x��intFn �Ƃ������Ƃ͊� f^(n) �� x �̋ߖT�łׂ�����0�ɂ������Ă邱�Ƃ��Ӗ����邩��
f �� x �̋ߖT�ő������B�����Ă��ꂪ�f���� D ��Ō����邩�猋�� f �S�̂��������A�Ɓc
�悭�ł��Ă�Ȃ�
>>165 �͌������
D���f���Ł�Vx��D��핢���ĂĂ���Vx=R�Ƃ͌����
D={������}, Vx=( [x], [x]+1 )
�̂Ƃ���Vx=R�_Z�ɂȂ��Ă��܂�
�ȉ�������
S = { U : open ; f ��U�̊e�A��������ő����� }
�Ƃ���
R = ��Fn������J�e�S���[�藝�����ꂩ��Fn�͓��_������intFn��S�ɑ����邩��S�͋�ł͂Ȃ�
�܂�S�̌��͍����ŕ��Ă��邩��ő匳������
�����U�Ƃ���
G = R�_U�Ƃ���
G���ӂƂ��Ė�����
�ĂуJ�e�S���[�藝���G��Fn�͓��_������
����ĊJ�W��V���Ƃ��ăӁ�G��V��G��Fn�Ƃł���
�܂�G��V�͌Ǘ��_�������Ȃ�
���̂Ȃ����c��G��V���Ǘ��_�Ȃ�(a,b)��G ��V= {c}�ł���a,b���Ƃ�邪����ɂ��f��(a,c), (c,b)�ɂ����đ�����������\���傫��m��(a,c),��(c,b)��f^(n)(x)=0��f��C^m������(a,b)��f^(m)(x)=0
�����f��(a,b)�ő������ƂȂ邪U�̍ő含����U��(a,b)���܂܂˂Ȃ炸c��R�_U�ɔ����Ă��܂�
�����G��V�͌Ǘ��_���܂܂Ȃ�
����a��G��V�̂Ƃ�m��n�Ȃ�m�ɑ�f^(m)(a)=0�ł���
�R����m�ɂ��Ă̋A�[�@�Ŏ������
m=n�ł͉���ɂ�萬������
m<k�Ő�������Ƃ���m=k�Ƃ���
a��G�_V���Ƃ�R���͌Ǘ��_�ł͂Ȃ�����ai��G��V�_{a}��lim[i]ai=a�ƂƂ��
���̂Ƃ�
f^(m)(a)
=lim[i](f^(m-1)(ai)-f^(m-1)(a))/(ai-a)=0
�ƂȂ�䂦�咣�͐�������
�Ō��V�ɂ�����f�͑������ł���
c��V,m��n�ɑ���f^(m)(x)��V��0�ɂȂ鎖�������Ώ\����c��G��V�̏ꍇ�͂��łɎ����ꂽ
c��V�_G�ɑ���c��(a,b)��V��f��(a,b)�ő������Aa,b�̂����ꂩ��G�̌��ƂƂ��
f^(deg(f))(x)��[a,b]��0�łȂ��萔������f^(deg(f))(a),f^(deg(f))(b)�͋���0�ł͂Ȃ�
�����deg(f)<n�ƂȂ�f^(m)(c)=0 (��m��n)�ł���
�����V��U�ƂȂ�G��V=�ӂł��邪V�̉���ɔ����遠
�܁H����������
����AR�̔핢R = ��Ui�������ĊeUi��f���������Ȃ�R�S�̂ő������ɂȂ�̂͊ȒP�Ɏ�����
�������̖�������͕K���������ƂȂ邩
>>177 �_���w�̖{�ɍڂ��Ă��Ȃ���
x=sqrt(2)^sqrt(2)�Ƃ���x���������Ɖ��肷���x^��2=2�����疳�����̖������悾���L����
x���L�����Ɖ��肷��Ɩ������̖������悾���L����
x�����������L������������Ȃ��Ă��ؖ��o����͖̂ʔ������
F_n���t�B�{�i�b�`����(������, F_1=F_2=1)�Ƃ���B
�ǂ����Ōv�Z�~�X���Ă��̂Ŗ������Ă�������
F_n���t�B�{�i�b�`����(������, F_1=F_2=1)�Ƃ���B
>>177 �L�������Ă������낭�Ȃ�
���Ⴊ����
�L�����̗L�����悪�L�����@����@1^1=1
f_n(x)=1/(��n-x)�Ƃ���
>>183 ���Q�͍��Z���ł�����������ƊȒP�ȗႪ���邾��
���̂���肷��˂�
�ʔ�����肨�����ā`�� 39���
http://2chb.net/r/math/1633923732/630 630 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2021/11/25(��) 20:48:12.16 ID:IXjS2eTu
�������̖������悪�L�����ɂȂ邱�Ƃ͂��邩?
�Ƃ��ǂ�������
>>184 1�������ԊO�ꂪ����܂�
>>181 Gn = ��[k=0��m](n-m-k)�EC[m,k]
l = n - (2m+5)
�Ƃ���
Gn
= ��[k=0��m](n-m-k)�EC[m,k]
= 2^m�~(n-m)-2^(m-1)m
= 2^(m-1)�~(2n-3m)
= 2^(m-1)�~(2l + m + 10)
F_(2l+2m+5)��2^(m-1)�~(2l + m + 10)
��F_(2l+2m+6)��2^(m-1)�~(2l + m + 10)
�� F_(2l+2m+7)��2^(m-1)�~(2l + 2m + 20)
��2^(m-1)�~(2l+2 + m + 10)
��l=0�̏ꍇ�����悢
��F_(2m+5)��2^(m-1)(m+10)�������悢
��F_(k+5)��2^(k/2-1)(k/2+10)�������悢
k=0��LHS = 5, RHS = 5
k=1��LHS = 8, RHS = 10.5/��2 = 7.424...
F_(k+5)��2^(k/2-1)(k/2+10)
F_(k+6)��2^(k/2-1/2)(k/2+10.5)
�̂Ƃ�
F_(k+7)��2^(k/2)(k/4+5+k/��8+10.5/��2)
��2^(k/2)( k/2 + 11 )
>>184 [[0,1],[-1,��n]]�̓���������x^2-��nx+1=0��������
n=1��x=exp(2��i/3)
n=2��x=exp(2��i/4)
n=3��x=exp(2��i/6)
n=1��x=1
�����n=1,2,3�Ȃ�P�ʍs��
n=4��u = [[1],[1]]���ŗL�x�N�g����v = [[0],[1]]��Av = v + u
A^12[u v ] = [ u v+12u] =[uv] [[1,12],[0,1]]
������[uv]^(-1)�������瓚��
>>185 (��2)^2log2(3)=3
(��2)^log2(3)=��3
����
>>184 �悭�悭�l������n=4�̂Ƃ��ŗL�l�Q�Ƃ�1�Ȃ���
[[0,1],[-1,2]]^k
= [[1,0],[0,1]] + k[[0-1,1-0],[-1-0,2-1]]
= [[-k+1,k],[-k,k+1]]
���
>>191 �ł��ł�
�s��v�Z�ɂ��ď�肭�ݏ�v�Z����Ƃ������ł���
���̌����ڂ���1,2,3,4�ő卷�Ȃ��悤�Ɍ�����̂��ʔ����ȂƎv���ďo�肵�܂���
�߂�����ȒP�Ȗ��
6n+2,6n+3,6n+4(n��1)��2��3�̔{���ɂȂ邩��
�ǂ��2n�̐����ɑ��Ă��A���̒���n�����܂��I�ׂΘa��n�̔{���ł��邱�Ƃ�����.
log[a] (log[b] (n)) = log [b^a] (n)
���{�l�̌��t�^�̊����͂��悻A�^40%,O�^30%,B�^20%,AB�^10%�Ƃ����B
�����炭�m�[�q���g�ł͖����Ȃ��
>>200 �X���`
���l��̓X���łǂ���
2���ȏ�̍D���ȑf�����v�������ׂĂ��������B
>>202 �X���`�A�Đ~���ē����o�����Ƃ��ł��Ȃ��悤���ˁB
���l���ł��T�N�b�Ɠ���������̂ɁB
>200�݂����Ȗ��͎��p�I�Ŗʔ����B
P(n-1,4)=��[i=1,n-3]��[j=1,n-3]C[n-1,i]C[n-1-i,j]0.4^i�~0.3^j�~0.2^(n-1-i-j)
>>206 ����
�~P(n-1)=��[i=1,4]P(n-1,i)
�ZP(n)=0.4�~P(n-1,1)+0.3�~P(n-1,2)+0.2�~P(n-1,3)+0.1�~P(n-1,4)
>>200 �����s���ŗՏ����������~�ɒǂ�����邱�Ƃ��Ƃ��ɂ͂���B
�W���[�X�łȂ��č̌��o�b�O�̌��ɂ����������A�����ȁB
���{�l�̌��t�^�̊����͂��悻A�^40%,O�^30%,B�^20%,AB�^10%�Ƃ����B
���̊�����100�l�̌����{�����e�B�A������Ƃ���B
���Ȃ킿A�^40�l,O�^30�l,B�^20�l,AB�^10�l�ł���B
����ׂ�1�l��I��ō̌�����4��ނ̌��t�����������I������B
�����l����̌����邱�Ƃ͂Ȃ��B
(1)99���̊m����4��ނ̌��t�����낦��ɂ͉��̍̌��o�b�O���K�v���H
(2)10�̍̌��o�b�O�����Ȃ��Ƃ���4��ނ̌��t�������m���͂����炩�H
>>203 �Ȃ��2���ȏ�H
5�ȏ�ł����̂ł́H�H
>>210 �������Ȗ��ő���
�i�摜�̉�b�l��������t���A�o��l�������j
�{���̏ē����A
>>205 �������o�����Ƃ͊ȒP��
�����炱�����̃X���Ɏ����킵���Ȃ�
>>201 �͑����m�[�q���g�ꂵ���̂Ńq���g
�܂� x = tan(��) �Œu�������
I(a,b) = ��[0,��]1/��((x^2+a^2)(x^2+b^2))dx
�����
I((a+b)/2,��(ab))
= ��[0,��]1/��((x^2+(a+b)2/2)(x^2+ab))dx
= 1/2��[-��,��]1/��((x^2+(a+b)2/2)(x^2+ab))dx
�R�����������u���ϕ�
�ǂ��u�����邩���~�\�ł��������܂ŗ�����̎�̐ϕ��̒u���̒��
�R�����s�^�b��I(a,b)�ɂȂ�̂��ƂĂ��S�n�悢
����
�G���f�V���̒藝������
>>201 >>215 ��Ԃ̒u��t=x+��(x^2+ab)�ł���
I((a+b)/2,��(ab))
= 1/2��[-��,��]1/��((x^2+ab+(a-b)^2/4)(x^2+ab))dx
�����Œu���@x = (t-ab/t)/2, dx = (1+ab/t^2)/2 dt ������
= 1/2��[0,��]1/��(((t-ab/t)^2/4+ab+(a-b)^2/4)((t-ab/t)^2/4+ab)) (1+ab/t^2)/2 dt
= ��[0,��]1/��(((t+ab/t)^2+(a-b)^2)t^2) dt
= ��[0,��]1/��((t^2+a^2)(t^2+b^2)) dt
= I(a,b)
���̊W������ȉ~���_�����ʂ����K�E�X�͐���
>>220 �f���炵��
�吳��
�����u��2����
J((a+b)/2,��ab) = 1/2( abI(a,b) + J(a,b))�d(❇︎)
�������܂�
�����܂łł����Ƃ��Ď���
���
a[n],b[n]��
a[0]=a, b[0]=b
a[n+1]=(a[n]+b[n])/2,
b[n+1]=��(a[n]b[n])
�Œ�߂�Ƃ�
J( a,b )/ I( a,b )
= ( a^2 + b^2 )/2 + ��[n:0〜��]2^n((a[n] - b[n])/2)^2
�ł��鎖�������Ă�������
----
(❇︎)���L�[�ł����R�������ł͖���
�Ƃ肠�����m�[�q���g��
�����������炭�m�[�q���g�͋ꂵ���ł��傤
>>218-219 �ʔ������Ȗ�肾���玩�͂ʼn����܂ł��̃X�����Ȃ��ł������Ǝv�������ǑS�������Ȃ�����X�����Ă݂���A�����������Ƃ�
�܂�2n-1�ł������邱�ƂɋC�t���Ȃ��ƃ_���������c
19�̐��̔{���ɂ����āA�e���̘a�̍ŏ��l�͉����H
>>224 �s�����ł�
���݂܂���
19����
1000...01�ō���̂ŊȒP�ł���
�Ȃ̂ʼn���
�ؖ������j�����ł����̂ł��肢���܂�
�f�p�ȋ^�₾����
�Ⴆ�A 59^59 �͉����ɂȂ�܂����H
���ɗ����ǂ����Ő��w������Ă�̂�
>>234 ��������Ȃ��B
�����A�e�ʂ̘a ��
�����ւ̉��p�����݂���Ȃ��Ǝv���������B
>>230 ����Ő����Ȃ�ł����A�ؖ������肢���܂�
>>236 ���݂܂���
�z����͔��z�����Ȃ�K�v�ł����A���Ȃ�̗͋Z�ł�����̂ŕ��j�����ł�k�ł�
����̒��w���p���̓e�X�g��������ǁA��������l���Ȃ��ċl��
���w23�N���̂��Z����ł悯��Ή�����H�����Ă����
3^n/2^n < k < (3^n-1)/(2^n-1) ����������n, k �����݂��Ȃ����Ƃ̏ؖ����A�����������
>>237 ���R�����njv�Z�@�}�^�[���
1���s�\�͎���
10^n��79�Ŋ��������܂��
[1,8,10,18,21,22,38,46,52,62,64,65,67]
��78�o�Ă��Ȃ��̂�2������
78-10^n��79�Ŋ��������܂��
[11,13,14,16,26,32,40,56,57,60,68,70,77]
��v���Ă�̏o�Ă��Ȃ��̂�3������
>>241 ���肪�Ƃ��������܂�
���݂܂���
10^n��79�Ŋ��������܂��
[1,8,10,18,21,22,38,46,52,62,64,65,67]
�����̃p�^�[�������Ƃ����̂͂ǂ̂悤�ɓ������̂ł��傤��
����3�������̌��_�ł����A1��2���g�����������o�Ȃ����Ƃ��ے肳���̂ł��傤���H
>>243 ���݂܂���O�����ȉ������܂���
�P���ɗ]�肪���[�v���邾���ł�����
>>243 10^m + 2�~10^n �� 0 ( mod 79 )���������Ȃ�
10^m + 10^n + 10^k �� 0 ( mod 79 )����������
10^m �� 78 - 10^n ( mod 79 )������������Ōゾ���ے肵�Ƃ��Ώ\���ł���
>>245 ���[�Ȃ�ق�
���炵�܂���
���肪�Ƃ�����������@������̂�
�������ł���
�p�ӂ��Ă����z����͎��̒ʂ�ł�
>>245 >10^m + 10^n + 10^k �� 0 ( mod 79 )����������
>10^m �� 78 - 10^n ( mod 79 )������������
�������悭�킩��Ȃ��B
10^(k+l) �� 1 ( mod 79 )
�ƂȂ�悤�ȓK���� l ���݂��āA
10^(m+l) �� 78 - 10^(n+l) ( mod 79 )
��������������Ă��ƁH
>>249 > �������悭�킩��Ȃ��B
> 10^(k+l) �� 1 ( mod 79 )
> �ƂȂ�悤�ȓK���� l ���݂��āA
> 10^(m+l) �� 78 - 10^(n+l) ( mod 79 )
> ��������������Ă��ƁH
�����Al �� -k ( mod 78 ) �������̐����ł悢
7�~143=1001
>>226 �̏o��҂ł����u41�v�̕����ǂ�������������܂����
41�̏ꍇ�A����5���ŏ��l�Ȃ̂ł���
���̏ꍇ��100021��1002001�A10003�A�Ȃǂ̉\����S�Ĕے肵�Ȃ��Ƃ����Ȃ��̂�
>>247 �̂悤�ɃO���t���_��p������@�̕����������y��������܂���
������[���T�������
f:(-1,1)��R��
>>256 �������܂�
f:(-1,1)��R��
f(x) = x-x^2+x^4-x^8+...=��_{k=0}^�� (-1)^k x^(2^k)
�ƒ�߂�.
�Ɍ�lim(x��1-0)f(x)�͑��݂��邩�H
�ł�
>>257 g(t) = ��[k=-��,��] e^(-��i(k+t)) x^(2^|k+t|)
�ƒu���Ƃ�g�͎���1�̊���
g(t) = ��[n=-��,��] a_n e^(2��int)
�ƃt�[���G�W�J�ł���
�W����
a_n = ��[0,1]��[k=-��,��] e^(-��i(k+t)) x^(2^|k+t|) e^(-2��int) dt
= ��[-��,��] x^(2^|t|) e^(-��i(2n+1)t) dt
= ��[1,��] x^u u^(-��i(2n+1)/log2) du/(u log2) + complex conj.
= ��(-��i(2n+1)/log2,-log x) (-log x)^(��i/log2) / log2 + complex conj.
�K���}���͋��������Ɋւ��Ďw���ŋ}��������̂ŁAg(0)�̎�v����n=0��
a_0��2|��(-��i/log2)/log2| cos(��log(-log x)/log2 + ��)
= 0.00274922168 * cos(��log(-log x)/log2 + ��) as x��1-0
���������ĐU������
>>259 �C��:�W���̎��̃~�X
a_n = ...
=...
...
�~ ��(-��i(2n+1)/log2,-log x) (-log x)^(��i/log2) / log2 + complex conj.
�Z ��(-��i(2n+1)/log2,-log x) (-log x)^(��i(2n+1)/log2) / log2 + complex conj.
�⑫:�Ƃ�arg(��(-��i/log2))=1.513321789...,
f(x)=x-x^2+x^4-...
�� 1/2 + 0.00274922168 cos(��log(-log x)/log2 - 1.513321789)
(x��1-0)
>>257 f(x)=x-f(x^2) --- (*)
x^4=1-��,0<��<1/2�ƒu����x-x^2>��/4���
f((1-��)^(1/4))=f(x)=x-x^2+f(x^4)>��/4+f(1-��)
������J��Ԃ���
f((1-��)^(1/4^n))
>f(1-��)+��/4+��/4^2+...+��/4^(n+1)
=f(1-��)+��(1-1/4^n)/3
��=0.1,n>2�Ƃ����
f(0.9^(1/4^n))
>f(0.9)+0.1*(1-1/4^3)/3
>0.9-0.9^2+0.9^4-0.9^8+0.9^16-0.9^32+0.9^64-0.9^128+0.1*21/64
>0.50058
����������(*)�ƍ��킹�čl�����
0.5���班�Ȃ��Ƃ�0.00058�̋����ŐU�����������Ȃ�
�t�[���G�W�J������ĕ��@�������
f((1-��)^(1/4))=f(x)=x-x^2+f(x^4)>��/4+f(1-��)
�ŏ���40�������Ă�f(0.9)��1/2����Ǝv���Ȃ�����
https://ideone.com/dW9xfg �����ƕ]�����Ă�̂�f(0.9^(1/16)) = f(0.993436601584)��
����ł��_�����ۂ�
https://ideone.com/2qGFH4 >>259 ,260
���[�ʔ�����@���肪�Ƃ��������܂��B
t�������Ď������ɂ��ăt�[���G�̗���͑S���v�����܂���ł���
>>261 ���݂��Ƃł��@�����炪�z�肵�Ă�����@�ł���
�ȉ��p�ӂ��Ă�����
�Ɍ������݂��Ă���Ɖ��肷��
f(x) = x-f(x^2)
��葶�݂���Ȃ�Ɍ��l��1/2
�����x��1�Ȃ�Ax^2��x���A
f(x) = x-x^2+f(x^4) �� f(x^4)
����ĔC�ӂ�a��1�ɑ���
f(a�j,f(a^(1/4)),f(a^(1/16)),...�͒P������
f(0.999) = 0.500125...
���Ɍ��l��1/2�ł��邱�Ƃɖ���
>>257 �̕ʂ̖ʔ����������̂œ\��܂�(Hardy, Divergent Series, p77���)
g(t) = f(e^t) - ��[n=0,��] t^n/(n!(1+2^n))
�͍P����
g(t) + g(2t) = 0
�����̂�g(-2^u)��u�̎�������
x��1-0��f(x)������ �� t��-0��g(t)������ �� g(t)�͒萔��
������g(t)��Re t<0�ʼn�͓I��
x��-0��Im g(x+2��i/3)����
(��Im ��^(2^k) = ��3/2 (-1)^k, ��=e^(2��i/3))
�ł���̂�g(t)�͒萔���łȂ�
����������lim[x��1-0]f(x)�͎������Ȃ�
>>267 ���ꂢ���Ă�H
f(e^t)
=e^t-e^(2t)+e^(4t)-e^(8t)+...
��re(t)<0�̂Ƃ��������邯��re(t)=0�̂Ƃ��������邩�̓A�[�x���̒藝���炢�����v�����Ȃ����ǃA�[�x���̒藝�Ȃ�W�J
f(x)
=x-x^2+x^4-x^8+...�[�@
�{�̂�x=exp(2��i/3)�܂ŘA���ɉ����ł��Ȃ��ƃ_���Ȃ̂ł́H
f(e^t)-��[n=0,��] t^n/(n!(1+2^n))
���萔�Ŏ������a��
��f(e^t)���������a��
�͂����Ă���������@��exp(2��i/3)�����ł��鎖�͐������ł���́H
>�{�̂�x=exp(2��i/3)�܂ŘA���ɉ����ł��Ȃ��ƃ_���Ȃ̂ł́H
�������킩����
�̑��a��2022�ƂȂ鎩�R���͑��݂��邩�H
>>271 n = 2^1011= 2x2x2x....
>>271 1346 = 2 * 673
(1 + 2)(1 + 673) = 2022
�悭�悭�l�����狕���̕������ɍs�����Ă̂��ςȌ�������������
���A����R������
�������A�����Ă���ɂ킩����
>>278 ����͂���������łȂ����H
f(e^z)=e^z - e^(2z) + e^(4z) - e^(8z) +...
�ɒ��Ӑ[��z=r+��i���������
��(r) = -e^r - e^(2r) + e^(4r) - e^(8r) +...
���Ǝv��
2��i/3�ł��܂������Ă��̂�
2^k��(-1)^k mod 3
�����藧����im((-1)^k e^((2��i/3)2^k))>0��������
>>279 ���A�ق�Ƃ�
�������ɂ����܂ŊÂ��͂Ȃ��̂�w
a>0�Ƃ���
>>274 1 + 2 + 673 + 1346 = 2022 �ł�����Ȃ��́H
>>271 �̑��a��2022�ɂȂ鎩�R����1346�̂P�����Ȃ����A
�̑��a��24�ɂȂ鎩�R����14,15,23��3������B
�̑��a��72�ɂȂ鎩�R����30�C46�C51�C55�C71��5������
�P����2022�܂ł̎��R����
�̑��a�����̐��ɂȂ鎩�R���������Ƃ������̂͂������H
>>283 2016��1440��21�ōő�
>>272 2^1011�̖̘a��4.38e304�Ȃ����̈Ӗ��킩���Ă�H
�����
>>287 �Ȃ��1�₻�̐����g�𐔂��Ȃ��́H
>>282-285 ������肪�Ƃ��������܂��B
���ɂȂ�܂����B
�A�z�ȏ������݂����Ď��炵�܂����B
���A���Ȃ݂Ɍ����Ȑ_�ˑ呲TOEIC700�ł� �u���P�[ �_(^o^)�^
�ӂ̒�����1,2,3,4,�c,95�̓K���ȕ��ёւ��ł���A���p���S�ē�����95�p�`�͑��݂��邩�H
�O
>>140 >>290 �g���P���g�v�X�����b�h�L���O�����ۂɂ͌������ƂȂ��B
�l�p�`�Ŏl�ӂ�1,2,3,4�ɂ��悤�Ƃ��Ă�4������Ȃ����A1,2,4,3�ɂ��Ă�3�̂Ƃ��낪��14
���ނ���ۂ��B
>>288 ���������̖̘a��1440��2016�ɂȂ�
��
552�̏ꍇ�F1+2+3+4+6+8+12+23+24+46+69+92+138+184+276+552=1440
2016�̏ꍇ�F1+41+47+1927=2016
>>289 ��͂�A������w���Ƃ̐l�͑��Ƒ�w��������Ȃ�
�A�r���܂���W�̓V���c���ł��邱�Ƃ��������Ă���B
>>290 �f���q���Q���邩�瑶�݂���
����L���Q�͔�����Q������������
>>295 �����ł�
���f���ʂ��g���A5�p�`��2��/19����]�����ē�������̏d�݂��悹��Ƃ�����@�ł���
�ǂ���1�łǂ���95�Ȃ̂����킩���
��������łȂ��Ă��悢
>>290 1�ӂ�1�̐�95�p�`��p�ӂ��A�ӂɏ��Ԃ�
0, 1, 2, ..., 94�̔ԍ�������
�ԍ���5�Ŋ������]�肪�����ӂ��Ƃ�
0, 1, 2, ..., 4 (�܂��� 0, 19, 38, ..., 76)
���猈�܂����l��ӂ̒����ɑ���
�ԍ���19�Ŋ������]�肪�����ӂ��Ƃ�
0, 5, 10, ..., 90 (�܂��� 0, 1, 2, ..., 18)
���猈�܂����l��ӂ̒����ɑ���
�ł������p�`�́A�p�̒l��ۂ����܂�
1�ӂ� 1, 2, 3, ..., 95 �̑��قȂ�l�̐}�`�ƂȂ�
5�p�`�~19�łȂ��A19�p�`�~5��
���������ꂼ��1,2,3,�c,9�̕ӂ��ǂ̂悤�ɑg�ݍ��킹�Ă��A���p���S�ē�����9�p�`�͍��Ȃ����Ƃ�����.
>>301 �Ȃ�قǂ��肪�Ƃ��������܂�
���f���ʂ��g��Ȃ������Ə����I�ȉ�@����������ł���
�O
>>291 >>303 1〜3�A5〜16�A17�A19��ӂ̐�����15�̃}�X�H�@�����H�@�ɓ������Ă��ƁH
����ĈقȂ鐔�Ȃ炠��9�����Ȃ����B
���������̎����Ă�
>>306 �Ⴆ�^�e1��4���̐����A�^�e5��3���̐������ĈӖ���
�O
>>306 >>303 ——————
3�b4�b6�b7
——————
9�b2�b0�b9
——————
1�b3�b7�b3
——————
7�b1�b9�b7
——————
231�����߂��B
>>309 �l�����Ƃ��Ă͂���Ȋ���
n�����R���Au��n�̑f���q�̐��Ƃ���
>>304 ��=exp(2��i/9)�Ƃ���
�S�Ă̌W����0〜8�̕��בւ��ł���8��������f(x)�ŃĂ����̍��ƂȂ�Ȃ����������悢
8���̍���0������悤�ɒ����ł���̂�7���������ŌW����1〜8�̕��בւ��Ƃ��Ă悢
f(x) = ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h
�Ƃ���
x^6+x^3+1�Ŋ��������܂��
g(x)=cx^5+(d-a)x^4+(e-b)x^3+fx^2+(g-a)x+(h-b)
�ł��邪�������R����0�ɂȂ鎖�͂Ȃ�
>>312 �������@�����ł��I
�ō�����0��t����̂͂��܂���
�Ă̍ŏ�������x^6+x^3+1�ɂ�����8���̑������ɂ���ƁA
(x^6+x^3+1)(ax^2+bx+c)
=ax^8+bx^7+cx^6
+ax^5+bx^4+cx^3
+ax^2+bx+c
�̌`�ɂ����Ȃ�Ȃ��̂ŁA���p�̓�����9�p�`��
���v����3��ނ̒����̕ӂ�3��J��Ԃ��`��������܂���
>>311 �Ō�
��[k=1,n]k^v ��^(��(k))=0�ƂȂ���̂����݂��鎖������
�̊ԈႢ�ł����H
�C�ӂ̐��̎������A���̎������ɑ��A
�C�ӂ̎����萔�Ȃ̂��A�����ϐ��im,n�̊��j�Ȃ̂��B
(X,d)�͊���������ԂŁAX�ɌǗ��_�͖����Ƃ���B
>>318 �̔w�i�F
(X,d)�͊���������ԂŁAX�ɌǗ��_�͖����Ƃ���B
����X�����X�Z�����Ȃ�AX �� ��_i {x_i} ��1�_�W���̍��X�Z�a�ɕ\���āA
�e {x_i} �� (X,d) �̕W���Ȃ̂ŁA�x�[���̃J�e�S���藝����A
���� {x_i} �͓��_�������ƂɂȂ�B���̂Ƃ��A{x_i} �͌Ǘ��_�ƂȂ��Ė�������B
����āAX �͔�Z�����ł��邱�Ƃ�������B
�]���āA�A���̉����̂��Ƃł́AX �͎����I�Ɏ������ȏ�ƂȂ�B
���́A���̂��Ƃ͘A���̉������g�킸�ɏؖ��\�ŁA���ꂪ
>>318 �̖��B
���̔w�i���������Ɠ�����Ɍ����邩������Ȃ����A
���ۂɂ͂��ƕ��ʂɎ�����B
>>319 +-�̗L����(�����܂�)�̑S�̂����Ƃ��ď������Ɂ��ʁ̃ʂ̓ɂ̌��ɂ�����+-��lj������`�œ����
���Ńp�����g���C�Y���ꂽ��Z�W���̑�F�ɂ�
�Ɂ��ʁ�F�Ɂ�F��
F�Ɂ�F�ʁ��Ӂ��Ɂ��� or �ʁ���
diam F�Ɂ�1/2^(len��)
�ƂȂ���̂��ȉ��̂悤�ɍ\������
�܂�F�ӂ͔C�ӂ̓_��I�т��̓_���S�̔��a1/2�̕��Ƃ���
�R�����Z�����Ȃ�
>>319 ��薵������̂Ŕ�Z�ł���
F�ɂ܂ō\������Ă���Ƃ���
F�ɂ���2�_x,y��I��x,y�𒆐S�Ƃ�������݂��ɑf�Ŕ��a��1/2^(len��+2)�ȉ��ɂȂ�悤�ɂƂ肻�ꂼ��F��+, F��-�ɂ���
��͂��Z�W���Œ��a�Ɋւ�������͖������Ă���
�c��̏����������̊m�F���e�Ղł���
C���肵�Ă���̂Ń��S�̂܂Œ�`�ł���Ƃ��Ă悢
���̖����������2^�ւ��邪�������:��1����2��...�ɑ��ĕW���̌�����F��1��F��2��...����܂芮������diamF�ɂ̏�������x����F��i����x���Ƃ��
�R����x(��)�Ƃ���Ƃ����قȂ錸����ЁA�т����F�ɂ̔��a���̉��肩��x(��),x(��)�͈�v���鎖�͂Ȃ�
�����X��2^�ւ��Z�x���傫���Ȃ�
>>315 ��>0��
| log[10](x) - log[10]�� | < ����|x-��|<��
�����悤�ɂƂ��(�� y=10^x�͘A��)
Kronecker���f���藝���玩�R��m,n��
|m log[10]2 - n - log[10]��|<��
�����悤�ɂƂ��
���̂Ƃ�
|log[10]2^m/10^n - log[10]��| <��
�����牼����
|2^m/10^n-��|<��
�ł���
>>321 �����I�\���̎d�����z����Ɠ����B
�W��S��n�̌������L���W���Ƃ���B
>>303 �B���
3461
6619
5479
9337
>>326 �v���O���~���O���Ƃ��Ėʔ�������
4�Ȃ��z���Ɠ]�u���ꎋ���ĉ��ʂ肠��́H
3�~3�̖����܂�ł邯��5�~5�̖��̈ꕔ�ɂȂ�H
>>326 10�i����Ȃ���8�i��16�i�Ȃǂ��Ƃǂ��Ȃ��
>>325 n=1 #f=1
n��2�ł͔C�ӂ̌݊���=(ab)�Ő������邱�Ƃ�����
a��b��
f(aa)=a,b�Ȃ�f(bb)=b,a, f(ab)=a,b�Ȃ�f(ba)=b,a
n=2 #f=4
n=3��S={a,b,c}
f(aa)=c�Ȃ�f(bb)=c
��=(ac),(bc)��f(cc)=a��b=f(cc)�Ŗ����Ȃ̂�f(xx)=x
f(ab)=c�Ȃ�f(ba)=c
��=(ac)��f(cb)=a,f(bc)=a
��=(bc)��f(ac)=b,f(ca)=b
f(ab)=a,b�Ȃ�f(ba)=b,a
��=(ac)��f(cb)=c,b,f(bc)=b,c
��=(bc)��f(ac)=a,c,f(ca)=c,a
#f=3
n��4��S={a,b,c,d,�c}
f(xx)=x
f(ab)=c�Ȃ�d=f(ab)�Ŗ���
x��y��f(xy)=x,y,f(yx)=y,x
#f=2^{nC2}
>>329 �ɂ���
n��4 �ɂ��Ă�����x�l���Ă݂�
�Ɨ��ɂ͑I�ׂȂ���
f(ab)=a,b�Ȃ�f(xy)=x,y��
>>332 �܂������������� �����ł�������
�W����̓��Z�őS�Ă̌��Ɋւ��đΏ̓I�ɂȂ���̂��l�������A
n���傫���ƑO�҂���҂�I�Ԃ����Ȃ��Ȃ邯�ǁA
��������Ώ����������ʂȂ��̂����݂ł���Ƃ������b�ł���
>>335 ���w�I�ɂ͈Ӗ��͖�������
n�~n�ɕK����������Ɩʔ���
�������S�̂̏W���� N �ƒu���B
>>339 (1)��(2)���瓱�����̂�(2)�̂ݎ����Ηǂ��B
(2) ���̐� �� �� �� = limsup[n����] |A��[1,n]|/n �ƒ�߂�B
������A���̐����� {n_k}_(k=1,2,�c) ���A
�C�ӂ̐��̐��� k �ɂ��Ď������藧�悤�ɒ�߂邱�Ƃ��ł���B
�n_(k+1) �� 2n_k
�|A��[1,n_k]|/n_k > ��/2
���̎��A
��_(a��A) 1/a
= ��_(a��A) ��_[1,��) |{a}��[1,x]|/(x^2) dx
= ��_[1,��) |A��[1,x]|/(x^2) dx
�� ��_(k=1,2,�c) ��_[n_k, 2n_k) |A��[1,n_k]|/(x^2) dx
= ��_(k=1,2,�c) |A��[1,n_k]|/(2n_k)
> ��_(k=1,2,�c) ��/4 = ��.
���ʏ�̊i�q�_���ȉ��̏����ŗL���F�ɓh�蕪�����Ă���B
���1�̐�n�p�`�^�̓��H�̊e���_�Ɏ��������Ă��āA�e���ɂ�0�ȏ�n�ȉ��̐��������������Ă���B
�����̏����H
>>344 ��ÂɌ��Ԃ����炱�̏�������Ȃ��ł��ˁB�������Ă�����đ��v�ł�
>>343 �u����Ă鎆�Ǝ����Ă鎆�̑g�݂���ԂƌĂԂƂ���
���[���ɏ]���Ĉ��̑�����ŏ��A������B�Ɉڂ鎖��A��B�ƕ\���Ƃ���
���[���ɂ́g�t����h����`�ł���A���Ȃ킿
�u�����Ă��鎆�Ǝ����Ă鎆���������A�����v���Ɍ����������ɏ����Ă鐔�������i�ށv�A���̑����B����A�Ɉړ����鎖��B��A�Ə����Ƃ���
�������A0����n�߂�A0��A1���d�Ƃ�m0= min{ m | ��n n>m, Am = An} �Ƃ�����m0=0�ł���A�łȂ����Am0=An, (n>m0)�ł���n���Ƃ�Ƃ�Am0��A(m0-1), An��A(n-1), Am0=A(n-1)����A(m0-1)=A(n-1)�ƂȂ�˂Ȃ炸�Am0�̍ŏ����ɔ�����
>>345 �܂�S�Ă̒��_�͓h���Ă�A������
���W��
>>346 ���݂܂���A�㔼�����̘_���܂������ł��Ă��Ȃ��̂ł����A�u�X�^�[�g����S�[���܂ł����̑���ʂ�s�����ꍇ�ƁA�t����̒ʂ�ɍs�����ꍇ�ƂŎ��̔z�u�������Ƃ͌���Ȃ�����(=���삪�������t�ɂ��Ĉ�Έ�Ή��Ƃ͌���Ȃ�����)�v�͌㔼�̘_�ɉe���͂Ȃ��ł��傤���H
�Ⴆ��A0=[0,2,1,3]��2���X�^�[�g�Ƃ��Č��̑�����s����[0,2,3,1]�̏�ԂŃS�[�����܂����A�t����ōs����[0,3,1,2]�̏�ԂŃS�[�����܂��B
>>348 �Ȃ�̎��H
��ԂƂ͌��̂Ƃ���ɖ߂�ł͂Ȃ������Ă鎆�A�����Ă鎆�A�o���Ă�ꏊ�A�S�Ă̏�ԂȂ���t�ł���ł���H
>>349 �@���Ⴂ���Ă܂����B�����ł�
�����`�̂�͂�����t�@���f�����F���f���̒藝�I�Ȃ��ꂩ
�N���Ƃ�Ɖ䖝�������Ȃ��Ȃ�
>>343 �O�O���ē������Ă��܂���
�R���͂����낢���ǐ�Ύv������
�܂������Ə����I�ȉ������̂��������
�O
>>309 >>343 0����n�܂ł̎��̖�����(n+1)�������琔���̘a�́A
n(n+1)/2
n���钸�_�̂�����ɂ�0�̎����u����Ȃ������ꍇ�A
�����̘a��n(n+1)/2�ŁA
n��n+1�̂ǂ��炩��2�Ŋ���邩�玩�R���B
��ӂ̑���͉\�ŁA
n�Ŋ��肫��邩��(n+1)/2���������_�܂Ői�ށB
n����Ȃ猳�̒��_�ɖ߂邪�����Ȃ�ʼn����̒��_�ɂ���B
n���钸�_�̂����ꂩ��0���u���ꂽ�ꍇ�A
n+1�����鎆�̂�����1�����u����Ȃ��B
���ꂪ0�łȂ��Ȃ�A���Ȃ킿n/(n+1)�̊m���ŁA
�u����Ȃ����̂Ԃ����̒��_�̈ʒu����O�̒��_�ɂȂ�B
�O
>>354 �����B
�u����Ȃ����̐������E���ɐi�ސ��ɓ��邩�����ς茳�ɖ߂�B
����342
>>356 ���1����Ȃ��Ă���������
���v���C���[�W����n=12�̂Ƃ�
���ʏ�ɉ~���^�����Ă���
>>359 ��K2�{�� L�� 90�x�������
�~�ɂ��Ԃ���B
>>360 ���܂�����������Ə����܂�
�E��K�́u2�_��ʂ钼���������v���삵���ł��Ȃ����ۓI�ȓ���Ƃ���
�E����ɂ����_�͑łĂȂ�
�E���Ɛ��̌�_�͐��m�ɑł��Ƃ��o����
�E����̓_�͖ڕ��ʂōD���ɑł��Ƃ��o���邪�A���m�Ȉʒu�͕s���Ƃ���
���Ǝ���܂�Ƃ��̃C���`�L���o���܂���
A=([0,1]�~(0,1)\Q^2)⋃(([0,1]��Q)�~{0})
>>359 �~�Ɛړ_���^�����Ă���Ƃ���
2�_�����Ԑ����̐���2��������`���菇������̂�
�~��ɂ���2�_�I���2�_���̐���2�������̌�_�Ƃ��ĉ~�̒��S������
������̓_�ɂ����钼����`���菇������̂�
���S�Ɛړ_�Ƃ�ʂ钼���ɐړ_�Œ������钼������������
>>358 �V�~�����[�V��������11 .5�����炢�ɂȂ����B
>>365 �u��K�̂݁v�łǂ�����Đ�����������}����́H
>>355 �������������Ȃ����琂����������}�����ʓI�ȕ��@�͂Ȃ��̂ł́H
>>369 ���ꂾ�ƃC�[�W�[������̂Ŗ����ł�
>>364 ����ʑ���Ԙ_�����[������ĂȂ��Ɠ������
>>364 �܂�f:[0,1]��A��(1/2,0)��im(f)�ƂȂ�Ƃ�im(f)��[0,1]�~{0}�ł���
�����łȂ��Ƃ���q���2�����ւ̎ˉe�Ƃ���m=sup(im(qf))>0�ƂȂ邪0<r<m�Ƃ���xi��[0,1]��lim(qf(xi))=r�Ƃł���
�K�v�Ȃ畔������Ƃ���lim xi = x���������Ă�Ƃ��Ă悢
���̂Ƃ�f(x)��A����qf(x)�͐��̗L�����ł��邪A�̌��ő�2���������ł���Ƃ�����͖������łȂ���Ȃ�Ȃ��̂Ŗ����ł���
����[0,1]����A�ւ̒P�˘A�����ʑ���(1/2,0)�ւ̒�l�ʑ��ƃz���g�s�b�N�Ńz���ƃs�[�ނ͂ЂƂ����Ȃ�
�����B�ւ̂���͓��l�ɂ���(1/2,0)�ւ̒�l�ʑ���(1/2,1)�ւ̒�l�ʑ��փz���g�s�b�N�Ȃ��̂����邪�A�����̓z���g�s�b�N�ł͂��肦�Ȃ�
���̂Ȃ���������Ȃ�pt��[0,1]��O�ɍ�������pt��(1/2,0)��pt��(1/2,1)���z���g�s�b�N�ɂȂ邪�r�������(0,1)��Q�ƂȂ�_���ʂ�Ȃ��̂ŕs�\�ł��遠
>>361 >�E����ɂ����_�͑łĂȂ�
�^����ꂽ�~���B��̋Ȑ��ˁH
>>375 �ړ_���^�����Ă���ꍇ�ł������܂���
�ЂƂ܂��ǂ��ł��D���ȂƂ���ɐڐ����Ђ��ō\���܂���
>>378 �����ł���
�����i�K�ł͉~��������������܂���
>>377 >>359 �̃q���g�Ƃ������Ƃł����H
>>381 �����ł�
�ȂȂ��ł����H
>>361 ����ɂ����_�͑łĂ�
2�_�����ƒ����������Ȃ�����
�ŏ��ɂ��邱�Ƃ͉~��ɓK����2�_����Ă����ʂ钼�����������ƂŊm�肩
���[��ނ�
>>382 �����ł�
�q���g��
>>363 �ɏ�����Ă��܂����A�p�X�J���̒藝�����p���܂�
>>385 �C���A�������ɂ��ꂾ���ł͂킩��Ȃ�
�����������Ȃ������܂�
>>386 >>383 �ɏ�����Ă��܂����A���̂悤�ɓK����(����䊐��ł͂Ȃ�)���`��`���Ƃ���܂ł͊m�肵�܂�
���Ƃ͂����̌�_���炤�܂��H�v�����܂�
���܂��q���g���o�������݂܂���
>>385 >�p�X�J���̒藝
6�p�`�ׂ̗荇��2���_��1�ɂ���Ƃ�����ʂ钼�����ڐ��ɂȂ���Ă��Ƃ�
>>388 �ցH
�ǂ䂱�ƁH
�������Đ\����Ȃ�
��������������Ȃ������܂�
�p�X�J���̒藝�̓R���ŊԈႢ�Ȃ��ł����H
>>391 �p�X�J���̒藝�͂��������ʂ�ł�
ABCDEF��Ȑ����6�_�Ƃ����Ƃ��A
�EAB��DE�̌�_
�EBC��EF�̌�_
�ECD��FA�̌�_
����3�_�͈꒼����ɂ���܂�
�}�������Ă��݂܂���
���̂悤��ABCDEF��z�u�����Ƃ��A
3�_�̈ʒu�W���ώ@���܂�
>>390 ���̓_�̑���4�_�����
���̓_��2�_�Ɗ��肵��6�p�`�̑Εӂ̌�_3�_��1�����ɕ��Ԃ���
���̓_�̑ΕӈȊO��4�ӂ�2�ӂ���6�p�`�Ƃ��Ă̑Εӂ̌�_�Ă���2��_��ʂ钼����
���̓_�̑Εӂ̌�_���
�������炻�̓_�Ɉ������������ڐ�
���t���ƕ�����ɂ�����
>>392 ���̏�Ԃ�E��D�ɋ߂Â��邱�Ƃ��l���܂�
���s���ƌ�_�����Ȃ�����
�p�X�J��16�ł��̒藝�ؖ������̂͂������V��
>>393 ������l�������ǃ_���Ȃ�Ȃ��́H
l1�͍���}����ĂȂ�����s��
�Ȃ̂�P����}���邱�Ƃ͂ł��Ȃ�
l2,l5�̌�_Q,l3,l6�̌�_R�͍�}�ł��Ă邩�炱��QR��̂ǂ�����P������
AF��u���Ƃ���B,C,D,E����蒼����B'C'D'E'�ɂ���ƐV����Q',R'�͍�}�ł��邯�ǂ��̒���Q'R'��l1�̌�_�͕ʂ̐V����P'�ł����Č���P�ł͂Ȃ�
�Ȃ̂�QR��Q'R'�̌�_��l1��ɂ���Ƃ͌���Ȃ�
>>392 �ɂ����āAE��D�Ƃ���ƁA����DE����}�o���Ȃ�
�Ƃ������Ƃł����ˁH
�p�X�J���̒藝���
�Ԑ��̌�_�A�ΐ��̌�_�A���̌�_���꒼����ɂ���
�Ƃ����̂��|�C���g�ł�
>>394 �_�����A�킩��Ȃ�
5�_�����Ȃ��ł���ˁH
�p�X�J���̒藝��6�_����ł���ˁH
A,B,C,D,E�̂ǂ����d�����ĂƂ��Ă�_�Ȃ�ł����H
>>399 �����܂���A�����~�Q�ł��A���ʂĂ܂���
����������������
5�_A,B,C,D,E�Ƃ��ăp�X�J���̒藝apply����Ƃ��ɂǂ�apply�����ł����H
�ǂ�2�_���Q��g����ł����H
>>401 ������܂���
��������܂�
����͂��̂悤��5�_��z�u���āA
�EDC��AF�̌�_
�EDF��EF�̌�_
�����Ԓ���L��`���܂�
����ɁA����AB��L�Ƃ̌�_��P
�Ƃ���Β���PD���ړ_D�ł̐ڐ��ɂȂ�܂�
PD���ڐ��ɂȂ闝�R��
>>392 �̒ʂ�ŁA
E��D�ɋ߂Â���킩��܂�
���߂�~�X�ł�
>>402 �C���A�����܂���A�ؖ��̕����m�肽����ł�
�{���p�X�J���̒藝��6�_���܂���ˁH
����������ĂQ���d���������ł����
6�_�̏��Ԃ�A,B,C,D,E,F�Ƃ��ďd������������A�Ƃ��܂�
�����Е���F(����B)�̏ꍇ�͊��ɏ������ʂ�Q,R�͍�}�ł��܂���P����}�ł��܂���
�����Е�������3�_�̏ꍇ�̓p�X�J���̒藝�̓g�[�g���W�[�ɂȂ��Ă��܂��ڐ����o�Ă��܂���
����
>>402 �Ő������ڐ��ɂȂ��Ă闝�R�̓p�X�J���̒藝���ǂ�apply������o�Ă����ł����H
>>405 �L���̐ݒ��
>>391 �������������Ɛ������܂�
�p�X�J���̒藝�̓R���ŊԈႢ�Ȃ��ł����H
�藝
�Ȑ���ɒ��_������6�_�����ɑI���ABCDEF�Ƃ���
����FA��l1,����AB��l2,...����EF��l6�Ƃ���
l1��l4�̌�_��P,l2��l5�̌�_��Q,l3��l6�̌�_��R�Ƃ����P,Q,R�͓��꒼����ɕ���
���ꂪ�p�X�J���̒藝
��{�u�אڂ���2�_�͑��قȂ�v�����Ǔ����Ɏ�����ꍇ�ł����̏ꍇ�́u���̓_�ɂ�����ڐ��v�ɓǂݒ����Ă��咣���̂͐������Ă�
>>406 >>392 �̐}�ɂ���ʂ�ADE������Ă���ꍇ��P�̍�}���\�ł���ˁH
E��D�ɋ߂Â���A�Ƃ����Ɍ�������l�����PD���AD��̐ڐ��ɂȂ�͖̂��Ȃ��Ǝv���̂ł����A
���ɂ����āA��_��P�A�Ԍ�_��Q�A�Ό�_��R
�Ƃ����Ƃ��A�p�X�J���̒藝�ɂ��PQR�͈꒼����ł�
E��D�̋Ɍ�����ɂ����Ă�PQR�꒼���オ����Ȃ����Ƃ��������
�Ƃ������ƁH
�������ɂ�������ƘA�����̋c�_��������Ƃ��Ȃ��Ƃ����Ȃ���������Ȃ�
>>409 ����Ƃ킩����
D��E���d����������ł���
�C�����ꂾ���ł�
�����������Đ\����Ȃ�
>>410 ���[�Ȃ�ق�
�L���̌�����������̂��ȁH
����Ȃ炢�낢���₱�����Ă��݂܂���
>>411 �悭����܂���
������A��F���d���������̂ɐ�������Ă���͍ŏ��̎����̐ݒ��D��E���d�������Đ������Ă邩��b�����܂Ōo���Ă����ݍ���Ȃ�
���ʂĂ܂���
>>400 ���������݂���������
>>394 �����ׂ�
>>413 ���Ȃ��̐��������_�@�͂܂��킩���ĂȂ�����
�ǂ����́H
>>371 �ɏ������悤�ɃR���p�X�����Ƃł��Ȃ��Ǝv���Ă���
��K�ň�����̂͒�������������
���ǁA
�~�ɏd�˂�悤��
�O�p�`ABC�Ɠ_P������Ƃ�,
�E���g���C�[�W�[�ŃR���b�c���
1�ɖ߂�Ȃ��ŏ����Ⴊ��n�Ƃ���
>>361 ���ƂŎv�����̂�����
���s�Ȃ��_�������
���s���ǂ����͌�_�����邩�ǂ����Ŕ��f����Ƃ����
�ق�Ƃɕ��s�ȏꍇ�L���̗��ꂩ�炷���
����s�\�ɂȂ�Ȃ�����
����ł��Ă���������
���̏ꍇ��蒼���Ƃ��Ȃ�����ƃJ�c�R�����C
���������������Ƃ�����
�_����鏇���H�v���ׂ��łȂ����Ȃ�
A�_�ɐڐ������Ƃ�
�܂�B�_����Ē���AB������
����AB��̉~�̊O����P�_�����
�~���C�_��PC���~�Ƃ�����_D�Ō����悤�Ɏ��(�����ɂ���ʂ̈ʒu�Ɏ���Ƃ����������K�v���Ȃ�)
����AC��̉~�̊O����Q�_��QD����BD
�ƌ����悤�Ɏ��(�����ɂ��K�v)
��_��E�_�Ƃ�����AC�ƒ���BE�̌�_(�������炱��͌���肻��)��R�_�Ƃ�
����PR�ƒ���DE�̌�_(�����������肻��)��S�_�Ƃ�����
����AS�����߂�ڐ�
�C�ӂɓ_�����Ƃ���
�����ɂ́A��}�ł��Ȃ���ˁH
>>429 �Ȃ���������ĂȂ��đ�
�����ł��m�I�ȃR�����g���悤�Ɗ撣�����̂���
�p��������
>>429 ���H
�ł���̂����ǁA�A�A
�Ȑ����2�_��ʂ钼���͍l�����邪
2�_��1�_�ɏd�˂���
�����ʂ钼���͖����ɂ��邩��
�ڐ��͍l�����Ȃ�����
���Z�����邠�邾��
�ڐ��͍l�����邯�ǁA��K�݂̂ō�}�͂ł��Ȃ��Ǝv���B
>>391 ��}���đ̊����Ă݂��B
>>342 [0..t-1]��[t]�Ɨ��L����
��������Q=[t]^n��t���W��L���g�ݍ��킹�_�I���C���A���邢�͒P�Ƀ��C���ł���Ƃ����̂�L�̌��͑S�ē��꒼����ł��肩�A���̒����̕����x�N�g���ŁA�������S��+1�܂���0�̂����ꂩ�ł�����̂��Ƃ��Ƃ��Ƃ���
���C���̍��W�̑��a���ŏ��ł���_���n�_�A�ő�ł���_���I�_�ƌĂт��ꂼ��L-,L+�ŕ\��
+1�ɂȂ鐬���ɑΉ�����i��{1..n}��L��active���W�A0�ɂȂ鐬���ɑΉ�������̂�fix���W�ƌĂ�
Q�̊e�_��r�F�ɓh�蕪�����Ă���Ƃ���
���̂Ƃ���s�̐��s�{�̃��C���̏W��{L1,...,Ls}��
�E�I�_Li+�͑S�ċ���
�ELi�͑S�ĒP��F�łȂ����ALi�_Li+�͒P��F
�E���z�F���͂��傤��s+1
�������̂Ƃ���
�咣�@�C�ӂ�r,t,s�ɑ���N(r,t,s)��I��ŔC�ӂ�n��N(r,t,s)��Q=[t]^n��r�F�ɂ��z�F����ɒP��F�̃��C�����܂ނ���s�̐�����悤�ɂł���
���邢�͓��l�Ȍ��������Ƃ���[t]^n���P��F���C������s�̐�������Ȃ��悤�ȍ��Xr�F�ɂ��z�F�����悤��n�͍��X�L�������Ȃ�
(��) (t,s)=(T,S)�Ɍ��肵�����̎咣����(T,S)�Ƃ���(t,s)�̑S�̂Ɏ��������������A���̏����Ɋւ���A�[�@�Ŏ���
�ؖ��ɓ���O�Ƀ�(T,T)����������Ƃ��C�ӂ�S�ɂ��ă�(T,S)��������n��N(r,t,r)�Ǝ���[t]^n��r�F�̔z�F�͏�ɒP��F���C���������ɒ��ӂ���
�܂���(1,1)�͖��炩
(t,s)<(T,S)�Ŏ咣����������Ƃ���(t,s)=(T,S)�̂Ƃ����l����
s=1�Ȃ�A�[�@�̉����胳(t-1,t-1)���������Ă��邩��n��N(r,t-1,r)�Ƃ����[t-1]^n�����R��[t]^n�̕����W���Ƃ��čl���鎖�ɂ����ɒ��ӂ����悤��[t]^n�̃��C��L��[t-1]^(n)�ɐ��������Ƃ��P��F�ɂȂ���̂��Ƃ��
���̎�L��[t]^n�ɂ����Ă��P��F�ł��邩�������͕�1�̐�ł���
�����s=1�̏ꍇ�Ƀ�(t,s)�������ꂽ
s>1�Ƃ���
�藝(Hales-Jewett) t,r��C�ӂɂƂ�Ƃ����R��N(r,t)��I��ŔC�ӂ�n��N(r,t)�ɂ�����[t]^n��r�F�ɂ��z�F���P��F���C�������悤�ɂł���
N��2�ȏ�̋����ł���Ƃ���B
>>439 ���肪�Ƃ��B���̒ʂ肾�����B
�C�����܂�
N��2�ȏ�̋����ł���Ƃ���B
���̎��A�ȉ��̏��������ׂĖ�����a,b,c�̑g�ݍ��킹�����ʂ肩�����߂�B
0��a��b��c��N
a + b �� c
b + c �� a
c + a �� b
a + b + c �� N
��jN=8�̎��A�ȉ���6�p�^�[�����l�����邽�߁A6.
1, 1, 1
1, 2, 2
1, 3, 3
2, 2, 2
2, 2, 3
2, 3, 3
����������
����̓����́A[x]��x���Ȃ��ő�̐����Ƃ��A
[ (N^3 + 6*(N^2) + 72)/144 ]
�ƂȂ�B
�O
>>355 >>359 �܂��^����ꂽ�~���K�łł������B���A
�����Ȓ�K�ʼn~�������Ă��Ă����܂�Ȃ��A
��K�����킶�킸�炵�Ă����A
���肬��~����K����͂ݏo�����͂ݏo���Ȃ����A
�Ƃ�����ԂŎ~�߂�B
��K�ɉ����Ē������������ꂪ�~�̐ڐ��ł���B
�C�i�͐}�`���ɎQ��������_��
>>441 �s�����ȊO�̉��҂ł�����܂���
���[��
>>361 ������������
�����ł�����K��2�_��ʂ钼������������u�����ł��Ȃ��v���ۓI�ȓ���Ƃ��Ă��܂�
>>429 �����������Ă܂����A
�Ɍ���������Ă���̂́u�ؖ��v�̍ۂł����č�}���̂͋Ɍ�����͈���Ă��܂���
��
>>402 �̒ʂ�ł�
���̃��X������ �ӂƎv�����̂����A�ؖ��̍ۂɋɌ����K�v�Ȃ��悤��
����͂��̎�̏����̖��l����Ƃ����ł��o�Ă�������
�O
>>441 >>443 �ق�2�_�Ƃ�Ȃ���B
��K���Ă��܂�2�_�Ƃ��Ă��ꌋ�炦�����B
�Ȃɂ��p�X�J����A����[���Ȃ��B
>>402 �悭�킩���
5�_�͓K���ɂƂ��H
D�ł̐ڐ���AB�����s�ł��邱�Ƃ����蓾�����PD��D�ł̐ڐ��ɂȂ�Ȃ��ꍇ������͖̂��炩����Ȃ��́H
>>447 �u��K�Ă�v�Ƃ������������Ƃ͂ł��܂���
�܂��Ăⓧ���Ȓ�K�Ƃ������Ă܂����A���S�ɘ_�O�ł�
>>361 �ɂ���ʂ�A
2�_��ʂ钼���������u�\�͂����Ȃ��v���ۓI�ȓ���ł�
���݂̒�K�ōl���Ȃ��ł�������
>>448 �������ɐԐ��������s�ɂȂ�ꍇ���܂����ł����A
���s�ɂȂ�����AD��B�̊ԂɐV����B�f��K���ɂƂ�悢�����ł�
a[n] = 2+��(2+��(2+��(2+�c��2))�c) (�オn��)�̂Ƃ��A
�O
>>447 >>449 ������5mm���̊i�q���B�d���B
���M���̃J�b�e�B���O�ɂ͎������Ȃ��B
�œK�ȃT�C�Y�Ɋg��ł���B
>>451 �v�Z�@�ł��Ǝ�������l�Ɍ����Ȃ����ǂق�ƂɎ�������H
https://ideone.com/JNT7sW >>453 2+��(2+��(2+��(2+�c��2))�c)��4
�Ȃ̂ł��������}�C�i�X�ɂȂ�Ȃ��Ƃ��������ł�
100���قnjv�Z�����
�n�������͒n���C��45�x�Ŏ��ł���炵���̂�
>>456 ��^2 = 9.869604401089358
�����
a1 = ��2
���A���������H
�ق��ACayley–Bacharach theorem �Ȃ�Ă��̂�����̂�
>>460 �������ł�
�l�����j���吳���ł�
>>459 ���݂܂���@������Ȃ�ł���
�N�I���e�B�͂܂��܂��ł�������
���\�͂��グ��悤�ɐ��i���܂�
>>457 1700���N��100�x�ɂȂ�Ɖ��肵�Ă�����x�v�Z������������
550�N��31�x���ϋC���͏㏸����̂�46�x�ɂȂ�̂�550�N��̖�2550�N
�n���͔N��0.06�x���ϋC���͏㏸���Ă���
1960�N�����猴�������Y����Ă邩�炱������550�N��Ȃ�2510�N�ɂȂ�
>>465 �����̍ō��C���̊�l��36�Ƃ����
1960�N����60�N���2020�N����
�����̍ō��C����0.06�~60=3.6�x��
39.6�x���L�^���邱�Ƃ��ł���悤�ɂȂ��Ă�
�Ƃ葊�o�ň�������
>>450 ���s�ɂȂ��Ă邩�ǂ����͒�K�����łǂ�����Ă킩��́H
���ɂ��������낢��肠������
>>473 ���{�l�ł��X�ɏZ��łĕ��l40�̍��Z�𑲋Ƃ�F���������̒Z�呲�ł�
��͂�����ō��ɂ������낢�Ǝv���ďo�����̂����������Ȃ��߂�Ȃ���
���ꂪ�킩��Γ��{���{�ɎY�߂摝�₹����Ȃ��Ƃ����Ȃ��Ƃ�
�O�̎��� f,g,h:R��R �̑g�ł����āA�C�ӂ̎���x,y�ɑ���
�ł���
>>478 �����I������
�i���l�ނƂ��o�Ă��Ĉ�u�g�\�������ǁA���e�悭�����炻��قǕ��G����Ȃ��Ăق��Ƃ������j
f,g,h�ɂ��Ă̏������̂������
�wy=f(x) �̃O���t�� x �������ɂǂ̂悤�ɕ��s�ړ����Ă��A
���X��_�̗�O�������� y=g(x) �̃O���t�Ɗ��S�ɏd�Ȃ�x
�ƕ\�����������킩��₷���������ȁc�Ə����������
���X�͕ʂ̖����l���Ă��r���ŏo�Ă�����肾�������ǁA
���{�I�ȊW���ɗL���̗�O����������ǂ��Ȃ�H
��悭�l�����畡���̊����o�Ă�������������Ă��܂��������ƂȂ���
���Ă��Ƃł������̕������C���Ŏ��グ�Ă݂Ăł������ł���
�������S�̂̏W���� N �ƒu���BA��N �� ��[a��A] 1/a �� �{�� �����Ƃ���B
>>480 0〜d-1����Ȃ����k�̐���bi��K���Ȑ�����������ĒP����������邱�ƂɂȂ邪���������̂��͍̂ő�k������鎖���ł��Ȃ�
����Ăł�������͂ǂ�Ȃɑ����Ƃ��ꌅ��k�A��k�A...
�ƂȂ�
����Ă܂��S����1�ł���ꌅ�̐���k�A���͑S����1��2���̐���k�A�d����ׂ������(ci)�Ƃ����ci��ai�ƂȂ�
���̂Ƃ���1/ai����1/ci�Ō�҂͐�Ύ�������̂ʼn���ɔ�����
�\����������r���L�����Ɖ��肵��r��d�i�@�ɂ�����z�����̎�����N�Ƃ����ƁA
>>481-482 �����I�����ɂ����ƁA�L�����Ȃ�
0.(��z��)(�z��)�E�E�E
�Ƃ����\�������Ă���̂ŁA�����Ȍ��͈̔͂ł́A�������̂��̂����������Ă���\���͂���B
�������A�\���傫�Ȍ��͈̔͂ł́A�������̂��̂͒萔�����Ȃ��̂ŁA
�ǂ݂̂� ��[a��A] 1/a �� �{�� �ƂȂ��Ė����A�Ƃ��������B
���Ȃ݂ɁA��[p�F�f��] 1/p �� �{�� �Ƃ����L���Ȍ��ʂɂ��A
�f����ɑ���
>>480 ���K�p�ł��Ė������ɂȂ�B
���̏ꍇ�̓R�[�v�����h�E�G���f�V���萔�ƌĂ�Ă���B
wiki���ƁA�R�[�v�����h�E�G���f�V���萔���������ł��邱�Ƃ��A
�Z�p�����藝��x���g�����̉����ɂ���ďؖ����Ă��邪�A
������y���Ɏア ��[p�F�f��] 1/p �� �{�� �Ƃ������������ł�������A�Ƃ������ƁB
�ԈႦ��
>>480 �̂���
�ł������������������ǂ�
���ʑ̂̊e�ʂ̖ʐςƓ������������@�x�N�g����S�đ�����0�x�N�g���ɂȂ邱�Ƃ�����.
�e�ʂ��O�p�������Ă����S�Ă̖ʂ͎O�p�`�Ƃ��Ă悢
>>489 ���[�������ł��@�f���炵��
�K�E�X�̔��U�藝�ɂ��ؖ���p�ӂ��Ă��܂������A
�l�ʑ̂ɕ������O�ς𗘗p
�͖ʔ����ł���
(-10^(-2(��/log10)^2) + 1/2) (2��/log10)^(1/2) 10^(1/8)
>>492 1.101001000099998...
�ō����Ă܂�
�Ȃ�S�R�������www
>>�ŏ��̕�1.1010010001�ňȉ��v�Z�덷���Ǝv������
�ǂ䂱�ƁH
1+(1/10)^1+(1/10)^3+(1/10)^6+(1/10)^10+...
������������
����
�Ȃ������H
>>491 �͐��U�@�ł͓���Ǝv���̂ł�����q���g���o���܂�
���̖��́A���
>>257 �̉�
>>259 �Ɠ������@�ʼn����܂�
�^�p�Y���{���
a[0] = 1, a[n+1] = a[n] + ��(a[n] + a[n]^2)
b[n]=a[n]/2^n�Ƃ���
>>506 �s����
�Ō�̍s���瓾����̂�2��=2���Ƃ������Ӗ��Ȏ��ł�
�������Ă݂���
>>509 2�{����Ă��� or 1������Ă��邪�A����������34�������Ă�
>>511 ����1/log(2)�H
�q���g���Ȃ������܂�
>>512 ���ɂȂ����C���ŋt���Ƃ��Ă݂�
>>513 �t��b[n]�̑Q������
b[n+1] = b[n] / ( 1+ ��(1+b[n])) )
�������Ȃ̌����ς�
�ł��킩���orz
b[ n + 1 ]= ��( b[n] - 1 )
������
���̑Q�����̖��ʔ����@�悭�v������
>>520 �������͊ȒP����
�ό`���Ă�������
�������͓��
�ǂ������ό`������o���˂Ȃ��
�ł��R���悭�l�b�g�Ō�������^�C�v�Ȃ��
>>503 ����ʔ�����
�}���قŌ������^�p�Y���{�ɍڂ��Ă�
����G���Ɍf�ڂ��ꂽ���Z�������̖��(�̉���)�Ȃ��NJ�ꂽ�̂ЂƂ��f���炵���Ă�����Ɗ�������
���̖{�Ȃ��Ȃ��ʔ������ڂ��Ă����ǂ���͖���̂ЂƂ��Ǝv��
���ʏ�ɔ��a�̈قȂ��̉~P,Q�ƁA���̒��SP,Q�����݂���B
>>359 �݂����Ȗ����������̂�
���S���^�����Ă邩���Փx��
>>359 �����ȒP����
���[����
>>361 �Ɉꉞ�u�����_��ʂ钼���������v������lj���
>>526 �ꉞ���̏�����ł킩�邩��킴�킴����Ȃ��Ă��������ȂƎv����
�����Ƃ����ق����悩�������ȁH
>>524 (1) ���߂�2�ڐ��̐ړ_��T,U�Ƃ���
T,U�����܂��������̍�}�@�͊��o
�܂�P��ʂ�~P��2�_A1,B1�Ō������钼��l1���Ƃ�
����A1,B1�ł̐ڐ�m1,n1������
���̌�_��R1�Ƃ���
���̂Ƃ�R1�͒���TU��ɂ���
���l�̍�Ƃ�������{�ʂ�l2��I��ōs��R2�����
����R1R2�Ɖ~P��2��_��T,U�ł���
(2)P,Q�̔��a��p,q�Ƃ���
p<q�Ƃ��Ă悢
���SP,Q��p:q�ɓ�������_�ƊO������_����}����悢
(1)�ɏ]��T����}����
P��ʂ�PT�ɒ������钼������}����(��q)
���̒����Ɖ~P�̌�_�̂�������PQ�Ɋւ���T�Ɠ������ɂ����_R����}����
PT��QS�̌�_��X�Ƃ����XSP�Ɓ�XTQ�͑����䂪p:s�̑����ȎO�p�`�ɂȂ�
������Ƃ�U�Ɋւ��čs�Ȃ��Β���PQ�Ɋւ���X�ƑΏ̂ł���_Y����}�����
XY��PQ�̌�_�����ʓ��ڐ��̌�_�ł���
��������(1)�̎菇�Őڐ���
�O���_�͒���PQ�ƒ���RT�̌�_��PQ��p:q�ɊO������_�ł���
�㔼����
>>528 P�͉~P�̒��S������m1��n1�͉~P�̐ڐ����Ƃ������_�����܂����H
���ƌ�q�Y�ꂽ
>>533 P�͉~�o�̒��S�Ȃ̂ŁA
�_�o��ʂ�~�o�ƌ�_�����`1B1�͒��a�ł�
�Ȃ̂ł��̕��@��m1,n1�������Ă����s�ł�
�p�̐ڐ��Ƃ����Ӗ��Ȃ�A�p�̊O���̓_�ł���m1,n1��ʂ���
�p�̐ڐ����������@�������ĂȂ��̂ł��߂ł�
>>538 ����������Q�ł̐ڐ��Ȃ����_A1,B1�͒����Ɖ~Q��2��_����H
>>535 >>528 �ʼn~�o�ƂȂ��Ă��̂Ŋ��Ⴂ���܂���
�~�p�̂��Ƃł���A�ꉞ�q1���s�t��ɗ���ؖ������肢���܂�
>>536 ����͂܂����w�̒���{�e�[�}���
���W���~��x^2+y^2=r^2�ƂȂ�悤�ɂƂ�
R1(a,b)�Ƃ���R1��ʂ�2�ڐ���2�ړ_��ʂ钼���̕�������ax+by=r^2
P�̍��W��(c,d)�Ƃ���ac+bd=r^2
�����c�_�t�����ɂ����������Ē���TU��R1��ʂ�
���w�ł͏ؖ����Ȃ��Ŏg�����炠�����낯�ǂ���Ȃ��w�}�j�A�ɂ͏펯�ł���H
>>537 ���J�ȏؖ��̕����������Ǝv�����̂�
�����Ă������肠�肪�Ƃ��������܂�
�u�ꉞ�v�ƑO�u���͂��܂������A�������Ɗ������炷���܂���
�����������v�ł���
���Ȃ݂ɕ���������܂�
���łȂ̂ł���̏ؖ�����W���܂�
xyz��ԓ���1��1�̗����̂�xy���ʂɐ��ˉe����Ƃ��A���̖ʐς��ő�ɂ���ɂ͗����̂��ǂ̂悤�ɔz�u����悢���B
>>542 �ނ������Ă킩���B�q���g���������c
�L�������
�藝�@���SO���aR�̉~�ɓ��ڂ���l�p�`ABCD�ɂ����Ē���AB�ƒ���CD�̌�_��X�A����BC�ƒ���DA�̌�_��Y�Ƃ���Ƃ�
���l�ʑ̂Ȃ�A���ςŌ��������ȁB
�����̂�|x|,|y|,|z|��1/2�Ƃ��Ă悢
���l�ʑ̂̎��͍ŏ��l�����
>>548 p���ĉ��H�ЂƂ̕��ʂɑ���n�̎����Ȃ�Ă�����ł��������A�ˉe�̖ʐ�n�ɑ��Ĉ��̒l(a+b+c)�ɂȂ���Ă̂��Ӗ����킩��Ȃ�
>>551 ���_���n�_�Ƃ��āA����a^2+b^2+c^2=1�̉��������I�_�Ƃ���悤�ȃx�N�g��������Ă��ł���B���̎������Ɗe���ʂɑ���(a, b, c)�͂�����ɒ�܂�B
�V�������c�̕s������(a, b, c)��(1, 1, 1)�ɑ��Ă���Ă�B
�ł����̖ʐς�a+b+c���Ă͉̂����킩���B
�ʐς�S�ł��镽�ʐ}�`��P�ʖ@���x�N�g�����m�̓��ς�m�̕ʂ̕��ʂɎˉe�����Ƃ��̖ʐς�|m|S
a����a,b,c��0��a,b,c��0�̂����ԈႢ
>>553 �����̂̎ˉe�����Ȃ炸�����`�̎ˉe�ɂȂ��Ă�Ƃ͌���Ȃ��Ȃ��H
���Ƃ��Ζ@���x�N�g���̎����ɂ���Ă͐����`�̎ˉe�Ɛ����`�̎ˉe���d�Ȃ邱�Ƃ����Ă��邾�낤���B
>>555 �����̂̎ˉe�͌����������Ă��鐳���`�R�̎ˉe
�܂�K���R�̕H�`�̍���
�����̘̂Z�ʂ̒P�ʖ@���x�N�g���͎O��ށB�������A
>>557 �Ȃ�Œ����Ȃ�
����Ȃ��ؖ��ł�����H�����͒������L�тĂ�����炻�̌������ˉe���ɍ��e�͈�_�̂�
����͍ŏ��ɓ�������������_�̂�
�����Č����̕����x�N�g���Ɩʂ̌����x�N�g���̓��ς����ł���ʂ����̓_���ŏ��Ɍ����ɓ����鎖�ȂǕs�\���H
����Ȏ�����̎̏ؖ��ŗv�������킯�Ȃ����
�A�z��
���[�N���b�h��Ԃ̎O�̒P�ʃx�N�g�� a,b,c��R^3 s.t. a�b=b�c=c�a=0 ���A
>>542 �����̂�1�̖ʂ��Axy���ʁAyz���ʁAzx���ʂɎˉe�������̖ʐ�(���ꂼ��AS1,S2,S3)��
���v�́A�����̑S�̂�xy���ʂɎˉe�������̖ʐςɓ�����
�l�����̒藝���AS1^2+S2^2+S3^2=1^2
���̏������ł́AS1+S2+S3�̍ő�l�́A��3�@(S1=S2=S3=1/��3�@�̎�)
�������S�̂̏W���� N �ƒu���B
>>562 A�̗L�������W���̗�Ai���ȉ��̂悤�ɒ�߂�
(1)A1�̓�[a��A]1/a>1�����悤�ɔC�ӂɂƂ�
(2)A(n-1)�܂ō\�����ꂽ�Ƃ���
�܂�A�_(A1���d��A(n-1))�̌������������̂��珇�ɕ��ׂ�b1,b2,b3...�Ƃ���
���̂Ƃ��e�ՂɑS�Ă�i�ɂ��ă�[j��i(mod n)]1/bj=���ƂȂ�
������[ j | j��1 (mod n)]�̗L�������W��F����[j��S]1/bj > 1�ƂȂ�悤�ɑI��An={ bj | j��S }�Ƃ���
�ł���(An)�ɑ���A'=��An�Ƃ���
�R�������߂��������
���ۃ�[a��A']1/a�͖��炩�ł���
�܂��C�ӂ�m>0��I�ԂƂ�����N��A�_[1,N]��A1〜Am�̌����܂܂Ȃ��悤�ɂł���
���̐�̍���m�Ɉ�̊����ł����Ƃ��Ă��Ȃ��̂�[N+1,N+T]�̒���A'�̌��͍��XTm+1��������Ȃ�
�����limsup A'��[1,n]/n��1/m�ł���
m>0�͔C�ӂł�����
>>562 ���Ȃ育���������Ă��܂������Ljꉞ��
���� n��0 �ƏW�� S��N �ɂ��Ď��� d(S,n) �����L�̂悤�ɒ�߂�
d(S,n) := |S��[2^n,2^(n+1))|/(2^n)
�i�Ӗ��I�ɂ͋�� [2^n,2^(n+1)) �ɂ�����S�̖��x�Ƒ����Ă��炦��Ɓj
(���P)
�W�� S��N �� lim_(n����) d(S,n) = 0 �������Alim_(k����) |[1,k]��S|/k = 0 �����藧�B
(�ؖ�)
���̐��� m ��C�ӂɌŒ肷��Bm��n ���� 2^n��k<2^(n+1) �̎�
|[1,k]��S|/k
�� |[1,2^(n+1))��S|/(2^n)
= d(S,n) + d(S,n-1)/2 + d(S,n-2)/4 + �c + d(S,n-m)/(2^m) + |[1,2^(n-m))��S|/(2^n)
�� d(S,n) + d(S,n-1)/2 + �c + d(S,n-m)/(2^m) + 1/(2^m)
�� 1/(2^m). (as n����)
����� limsup_(k����) |[1,k]��S|/k �� 1/(2^m) ���������B
m �͔C�ӂł��������� limsup_(k����) |[1,k]��S|/k = 0. �䂦�Ɏ����ꂽ. (���P�I)
������A���� A �����P�̉�������Ȃ�� A'=A �Ǝ��Ηǂ����Ƃ��킩��B
�ȉ��AA �����P�̉�������Ȃ��Ƃ���B���Ȃ킿
r := limsup_(n����) d(A,n) > 0
�Ƃ���B
���� {q_n} �ƏW�� A'��A �����̂悤�ɒ�߂�B
�܂� q_1 = 2 �Ƃ���B
(i) d(A,n) �� r/q_n �̎�
d(A',n) = d(A,n) �ƂȂ�悤�� A'��[2^n,2^(n+1)) ���߂�B
�܂�A��� [2^n,2^(n+1)) �͈̔͂� A �� A' �͓���Ƃ���B
�܂��Aq_(n+1) = q_n �Ƃ���B
(ii) d(A,n) > r/q_n �̎�
d(A',n) �� r/q_n �ƂȂ�悤�A��� [2^n,2^(n+1)) �͈̔͂� A ����ŏ����̗v�f���팸����B
�܂��Aq_(n+1) = q_n + 1 �Ƃ���B
���̂悤�Ɋe n �ɑ��� A'��[2^n,2^(n+1)) �ɑ�����v�f�����߂Ăł����W���� A' �Ƃ���B
>>562 �̑���
r �̉��肩�� (ii) �̃p�^�[���͖�����N���邱�Ƃ��ۏ����̂ŁAlim_(n����) q_n = ��.
�䂦�� lim_(n����) d(A',n) �� lim_(n����) r/q_n = 0 �ł��邩��AA' �͕��P�̉�������B
�܂��Ad(A,n) > r/q_n �������� n �S�̂����������� {n_k}_(k=2,3,�c) �ƓY���t��������ƁA
q_n �̒�`���� q_(n_k) = k ���������B
��� d(A,n) > r/q_n �̎��� A' �����菜���ꂽ�v�f�͍ŏ����ł��邩��
|[2^n,2^(n+1))��A'| = [(2^n)r/q_n] > (2^n)r/q_n - 1
�ƂȂ�B�������
��_(a��A') 1/a
�� ��_(n=0,��) ��_(a��A'��[2^n,2^(n+1))) 1/2^(n+1)
> ��_(n=0,��) 1/2^(n+1)�((2^n_k)r/q_n - 1)
�� -1 + ��_(k=0,��) 1/2^(n_k+1)�(2^n_k)r/k
= -1 + ��_(k=0,��) r/(2k) > ��.
�ȏ�ɂ�莦���ꂽ�B
>>565 �̂���
> ��_(n=0,��) 1/2^(n+1)�((2^n_k)r/q_n - 1)
�̍s�͖������Ăق����B�폜�R�ꂾ�Ǝv���
>>503 �藝
(ai)��n�̐��̖���Ȃ钷��n�̗L����ł���A���̕�����ő��a�����傤��n�ƂȂ���̂��Ƃ��
���@�藝�ɔ��Ⴊ����Ƃ���
���̑��a���ŏ��ƂȂ锽����Ƃ�Ƃ��Aa��1�łȂ����̍ŏ��l�Ƃ����1�̌���a-2�ȉ��ł���
(��) �ŏ�����ɂ�����ai>1�ł��鍀�ɑ��Ă��̍����܂܂Ȃ�������S�̂̒��ō��̑��a��n�ȉ����̑S�̂̒��ɂ����鍀�̑��a�̍ő�l��mi�Ƃ����A���Ȃ킿
mi
= max{ ��[j��J]aj | J��i���܂܂Ȃ��A��[j��J]aj �� n }
�ł���
���̂Ƃ�mi=n-1�ł���
���̂Ȃ�͂���mi<n-1�ƂȂ�i������͂���ai��1�Ɍ���������������������A�����a���^�Ɍ���̂ōŏ�����ł��邱�Ƃɖ�������
����1�ł��鍀��mi���\�����鍀�S�ĂɊ܂܂�Ȃ���Ȃ�Ȃ�
�܂�a=ai���P�łȂ����̍ŏ��l�Ƃ�1�ł��鍀��a-1�ȏ゠��Ƃ����mi���\�����鍀�̒���1��a-1�ȏ�Ȃ���Ȃ炸�A��������a-1��1����菜�������ai��lj�����Α��a�͂��傤��n�ƂȂ�(ai)������ł��邱�Ƃɖ������遠
(�藝�̏ؖ�)
������m�̖ł��鍀�������m�ȏ�c���Ă���Ή��肩�������g���a��m�ƂȂ镔������Ƃ��̂Ŗ�������
>>523 ���̖{���ăs�[�^�[�E�B���N���[�̃p�Y���{�H
>>570 �����A�t�����N���̕��ł�w
�ɂԂ���
>>571 �s�[�^�[�E�t�����N������
���ꂪ���w���̍��A�r�[�g��������TV�ɏo�Ă��ȁB
���̐l�A���͉����Ă�낤�c�B
>>573 69�݂��������狳�E����͑ނ��Ă�����ł��傤��
>>572 ���t�����N���{�ɍڂ��Ă����ł�
�����
>>503 ���₳��������
�ǂ�������������{�����܂��Ƃ�����Ȃ���
�������ĕ�����ɂ�����
�ʃX���̖����
>>579 ����P�����̂悤�ɒ�`����B
�uP�Ȃ��2�͖������ł���B�v
P���U�ł���Ɖ��肷��ƁA
�uP�Ȃ��2�͖������ł���B�v�͐^�ł���B
�����P���U�ł��邱�Ƃɖ�������B
�]���āAP�͐^�ł���B
���܁AP���uP�Ȃ��2�͖������ł���B�v���^�Ȃ̂ŁA
modus ponens����2�͖������ł���B
1�ӂ̒�����L�̗�����ABCDEFGH��AG��ɓ_P�����B
L=1�Ƃ���
a[1] = 1/��2,
>>585 (2��a)/(1+a) = (1��a�̊���) / (1��a�̎Z�p����)
��
>>201 �̐ϕ��ƑQ����
>>586 �S�R�킩��܂���
���������ڂ���
K(x)�Ƃ��o�Ă����ł����H
���A�������Ȃ�ق�
�_����
���������q���g�o���܂��B
����H
����A�Ȃ�
>K'(x)=2/(1+x)K'(2��x/(1+x))
�O
>>452 >>581 �ő�l��V�A�ŏ��l��v�Ƃ���ƁA
�s�^�S���X�̒藝���A��FH�̋����́�(1+1/2)=��(3/2)
�ŏ��l��^����_P��FH�̋�����(��2/2)(1/��3)=1/��6
��V=��(3/2)��2(1/3)=��2/2
v=��(1/6)��2(1/3)=��2/18
>>590 �܂������قƂ�Ǔ����݂����ȃq���g��������߂ē��������̂��Ȃ�Ȃ��ǁA�q���g���Ȃ�����������ꉞ����������
K(x) = ��[0,��/2]1/��(1-x^2(sin(t))^2)dt
�Ƃ���
�u������
K(x) = (1/2)��[0,1]1/��(u(1-u)(1-x^2u))du
����Œ����̃I�C���[�̐ϕ��\������
2F1(1/2,1/2,1; x)
=��(1)/(��(1/2)��(1-1/2))��[0,1]u^(1/2-1)(1-u)^(1-1/2-1)(1-xu)^(-1/2)du
=1/��[0,1]u^(-1/2)(1-u)^(-1/2)(1-xu)^(-1/2)du
�ɂ��
K(x) = ��/2 2F1(1/2,1/2,1; x^2)
�ł���
�����log(1+x)�̃}�N���[�����W�J�ƃI�C���[�̐ϕ��\���ɂ��
1/x log((1+x)/(1-x))
= 2�E2F1(1,1/2,3/2,x^2)
= 2��(3/2)/(��(1)��(3/2-1))���0,1]u^(1-1)(1-u)^(3/2-1-1)(1-x^2u)^(-1/2)du
= ��[0,1](1-u)^(-1/2)(1-x^2u)^(-1/2)du
�ł��邩��
2K(x)-log((1+x)/(1-x))
= ��[0,1](1-xu^1/2)u^(-1/2)(1-u)^(-1/2)(1-x^2u)^(-1/2)du
= ��[0,1]��(1-x^2u)/(��u��(1-u)(1+x��u)du
�ł���
�ϕ��j��u��(0,1),x��[0,1]��
����
�����Ƃ��������j�]������O�̂�����c���Ă�������
�����ƁA
>>595 >>596 �̉�
> K(x) = ��/2 2F1(1/2,1/2,1; x^2)
�̃�/2���r���Ŕ��������ĂȂ��H
������
lim log(1-a[n])/2^n = -��/2
�ɂȂ�͂�������
���A�ق�Ƃ������Ă��
�C��log((1+x)/(1-x))�̑O��1/2�����Ă�orz
�C�������ĂȂ��A�����Ă�
x��1�ł��������Ă�
https://www.wolframalpha.com/input?i=lim+%5Bx%E2%86%921-0%5D+%282K%28x%5E2%29%2FK%27%28x%5E2%29%2Blog%281-x%29%2FK%27%28x%5E2%29%29& ;lang=ja
�����������̒l�́�2^n (n����)�ŏ����Ă��܂�����������邾���ŏ\���Œl���̂��̊W�Ȃ���
������2K(x)/K'(x) �� 2atanh(x)/K'(x)��x��1-0�ł́����L�����Z������̂͂��̒l�̔�ȊO���肦�Ȃ���
>>596 �̉�����10�s�ڂ̍��F log(1-x)/K'(x)
�����̉���f(x)�̎��� K'(x) �������Ă���̂�
�S�̂Ƃ��� K'(1)=��/2�{����Ă���
>>606 �����A�ق�Ƃ�
������thx
�ł��ʔ����˂��̖��
>>607 ����J�l�ł��B
�������C�����邾���ł悢�̂Ő����Ƃ��܂��B
���Ȃ݂�
>>584 �̓����̐���
lim log(1-a[n])/2^n = -��/2
�𐔒l�I�ɂ���ɂ͏��Ȃ��Ƃ����猅�̐��x�̌v�Z���K�v�ɂȂ�܂��B
������
>>605 �� log(64)/�� �̕����������
lim log((1-a[n])/8)/2^n
�Ƃ���Ƃ��̋Ɍ���agm�Ɠ����X�s�[�h(2������)�� -��/2 �Ɏ������܂��B
200���ł���Ă݂���-1.56267...�ŃM�u���Ă�w
>>572 ������2k��1,3��2��������Ȃ�~�����i�����ڂ�j�����ڂ�j��i+n(mod 2n)�̎��K���Ⴄ�����ł�����̂Ώ̉~����ƌĂ�
���@����2k�̔��Ώ̉~����̒��̘A������1�̌���x�Ƃ����x��k+1 (mod 2)�ł���
(��) �g�O���h�ɂ���אڂ���1-1�̐���p�A3-3�̐���q�Ƃ����x=p+q�ł���
����đO���ɂ���אڂ���1-3�܂���3-1�̐���k-x�ł���
�O���̊J�n�ƌ㔼�̊J�n�͈Ⴄ����������O���ɂ���אڂ���1-3�܂���3-1�̐��͊�łȂ���Ȃ�Ȃ�
�����k-x�͊�ł��遠
���̉�
���Ⴊ����Ƃ���
�ǂ����̉~�ʂ��琳�̌����ɒ��S�p���Ƃ̒l����ׂ�1,2,3�̒l����Ȃ钷��3k�̐���łł����~������l����
����ł͒����Ƃ̉~�ʂ̒��S�̌��_�����Ώ̂̈ʒu�ɂ͒���3�Ƃ̉~�ʂ̒��S�ɂ���K�v�����邩��A���̉~����2����菜����1,3�݂̂̉~������l����Ɣ��Ώ̉~����ɂȂ�K�v������
����Ă��̉~����ɂ͗אڂ���1-1�̌���x�Ƃ����x��k+1(mod 2)�ł���
���̉~�����2��2k�����Č��̉~���������ɂ�1-3���אڂ��镔���ł́g���Α��h�ɂ�����3-1���אڂ��镔���ɂ͓�����2�������Ȃ���Ȃ�Ȃ�
�܂������ꂩ��1-1�ł����Е���3-3�̕����ɂ�1-1�̕��ɂ�3-3�̕���肿�傤�Lj����2��������K�v������
���̏��������悤��2����������������ꂽ2�̐���l�Ƃ����l��x (mod 2)�ƂȂ�
����ĉ�����2�̌�l��l��k+1(mod2)�łȂ���Ȃ�Ȃ����A��ӂ�������2�̐���k�łȂ���Ȃ�Ȃ��̂ŕs�\�ł��遠
�O
>>594 10!=6!7!
10�~9�~8=6�~5�~4�~3�~2
=(5�~2)(3�~3)(4�~2)
>>609 ������ƑQ��������������100����20���܂Ōv�Z
https://ideone.com/Wd2SoK -1.5707943436849058509551755165447994552805531726447795866981023677557487181073360771069987343969219945e0
�^�l��-1.570796326795������6�����������ĂȂ�w
���̖��p�ɐ��l�v�Z���[�`�����`���[�j���O��������Ƃ����邾�낤���ǂ����܂ł��C�͂Ȃ��Ȃ�
a[1] = 2,
>>615 c=��(a[1]b[1])�Aa'[n]=a[n]/c�Ab'[n]=b[n]/c�Ƃ�����
a'[n]b'[n]=c^2�Aa'[n+1]=(a'[n]+1/a'[n])/2�Ab'[n+1]=2/(b'[n]+1/b'[n])
�� a'[n] = coth(2^(n-1)��1)�Ab'[n] = coth(2^(n-1)��1)�A��������1=atanh(a[1]/b[1])
�� a[n] = c coth(2^(n-1)��1)�Ab[n] = c tanh(2^(n-1)��1)
�� log(a[n]-b[n])/2^n
= log ( c coth(2^(n-1)��1) - c tanh(2^(n-1)��1) ) / 2^n
〜log ( coth^2(2^(n-1)��1) - 1 ) / 2^n
〜log exp (2^n ��1)/2^n
〜��1 = atanh(a[1]/b[1])
>>616 �����ł��ˁB�����~�X�i��1=acoth(��(a[1]/b[1]))�ł��� �j������܂��������ł��B
�G�������l�C�Ȃ������R�[�i�[
�t�����N���{���
5/2^4+6/2^5+7/2^6+...=3/4<1
�قړ����ɉ�����y�O�\���e�B�A�̖��
>>619 �ߋ��X���ɂ������悤�ȂȂ������悤��
���邩��
�ߋ��X���Ɏ����悤�Ȃ̂������āA
������
>>620 �̂悤�ȕs�ϗʁE�����ʂ̂����ł͔����ɉ����Ȃ��āA
Grundy�����������g���Ɖ�����A�݂����Ȃ̂��������C������
�����ʂʼn����܂�
�u�ʔ�����肨�����ā`�� �\�O��ځv�ɂ������B
806 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 16:39:41
���W���ʂ̌��_(0,0)�ɋ��1�u���A
���̃��[���ɏ]���ċ�̔z�u��ω������Ă����Ƃ���B
���[���F
���ʏ�ɒu����Ă����i���W(x,y)�j��1�I�сA���̋����苎��A
�V����2�̋�����ꂼ��(x+1,y)��(x,y+1)�ɒu���B
���̃Q�[���̖ړI�́A0��x��2, 0��y��1�͈̔͂�����ǂ��o�����Ƃł���B
�ʂ����Ă���͉\���낤���H
807 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 16:40:52
>>806 ���[���lj��B
(x+1,y)�܂���(x,y+1)�̂ǂ��炩�Ɋ��ɋ�u����Ă���ꍇ�́A
(x,y)�̋��I�Ԃ��Ƃ͂ł��Ȃ��B
808 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 17:27:14
���o�������悤�ȋC������ȁB �����A������ߋ����O���Ă݂��B
809 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 18:13:20
���o�B
�ŏ��̋���d��1�̔S�y���Ǝv���A������ɂ��A�S�y���ɕ������
�v�����Ƃɂ���B���̂Ƃ��A������J��Ԃ��Ă����ʏ�̔S�y�̏d����
�a��1�ł���A�����A0��x��2, 0��y��1�͈̔͂�����ǂ��o�����Ƃ����
�d���̘a��1��菬�����Ȃ��Ė����B
810 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 19:44:12
���Ⴀ�A(0,0),(1,0),(2,0),(1,0),(1,1)�ɋ�����悤�ɂ��邱�Ƃ͉\���H
814 ���O�F�P�R�Q�l�ڂ̑f������F2008/03/18(��) 21:08:49
(0,0),(1,0),(2,0),(0,1)(0,2)
����ǂ�������(1,1)�Ɏc�����Ƃ͉\������
�s�\���Ƃ���Ώd�������Ŏ������Ƃ͂ł��Ȃ���
��₩��
>>627 ����̉��ǂ̃^�C�~���O�Œ��ꂽ���͕�����Ȃ�
���Ȃ莞�����߂��Ă�����������܂�Ă��C������
�������A
>>625 �Ō������Ƃ���AGrundy�����������g����������
���Ȃ��Ƃ��A�����ʂɂ��͍��܂ł�1������ĂȂ��Ǝv��
�����ʂʼn�����Ȃ�m�肽��
�Ȃ�ق�
�����ʂʼn������Ăǂ��������ƁH
>>630 ��������
�Ⴆ��
>>619 �̖��Ȃ�
n�i�ڂ̃|�e���V������(1/2)^(n-1)�Ɛݒ肷��
n�i�ڂ̌�����菜����(n+1)�i�ڂ�2�lj����Ă����G�l���M�[�͕ω����Ȃ�(�����͂��Ȃ��ŏ\��)
�����z�u�̑��G�l���M�[��1
�T�i�ڈȉ��̃|�e���V�����G�l���M�[�̑��a��
5/16+6/32+7/64+�d=3/4
�Ȃ̂łS�i�ڂ܂őS��������͕̂s�\
>>627 �̖��Ȃ�_(a,b)�̃|�e���V������((��5-1)/2)^(a+b)�ɂ���ΗႦ��x��4,y��4�̑��G�l���M�[��1�����ɂȂ�̂ł��ꂾ���ŏI���
�ł�
>>627 �̖�肻�̂܂܂��Ə��Ȃ��Ƃ����̃|�e���V�����̐ݒ�ł͖���
https://www.wolframalpha.com/input?i=Table%5B++N%28%28%28%28%E2%88%9A5-1%29%2F2%29%5En+-%28%28%E2%88%9A5-1%29%2F2%29%5E%282n%29%29%2F%281-%28%28%E2%88%9A5-1%29%2F2%29%29%5E2%29%2C+%7Bn%2C1%2C10%7D%5D& ;lang=ja
�Ă����������\�Ȃ�Ȃ���
���A�z���g���y�b�O�\���e�B�A����Ȃ��̂�
�����
>>627 �ł���
�ł������[����
�������Z���Ȃ�l���Ă��珑����
>>580 ������Ă����閽�肪�^�ł��邱�Ƃ��ؖ��ł�����
�ǂ�������������H
>>636 �����P���U�ł��邱�Ƃɖ�������B
���������Ȃ��̂ł́H
���₻���͖��Ȃ���
>>638 >���Ȍ��y�^����
���肶��Ȃ����
�����
�J���[�̃p���h�b�N�X���ČĂ�Ă�����
�Ă�����Ȃ��傤���Ȃ��b����������
Blackpenredpen
�r���������藧���Ȃ�������Đ��w�̖��肶��Ȃ���Ȃ����ǂ�
>>645 �y�A�m�̌����n�̃w���N���X�ƃq�h���̖���Ƃ�������ł�����ł���
�Ă�����Ȃ��傤���Ȃ��b����������
>>627 ���Ȃ�Z���Ȃ���
�ȉ��������o�I�ɑ����₷�����邽�߂Ɂ���������4�����Ŋi�q�_�ɐ̒u���ꂽ��Ԃ�\������
���ꂼ��̕����̈Ӗ���
���d���ݐ����邪�����ꂻ�̃}�X�͊J���Ȃ���Ȃ�Ȃ�
���d���ݐ��Ȃ����ŏI�I�ɂ��Ȃ���Ȃ�Ȃ�
���d���ݐ͂��邪�����n���Ȃ��Ă��悢
���d���ݐ͂Ȃ��ŏI�I�ɖ����n���Ȃ��Ă��悢
�ł���
����ƌ��̖���
�������������@
�������������@
�������������@
�̂悤�ɕ\�������A��������ɂ͏����Ȃ��̂ʼnE���A�㑤�ɂ͖����́�������ł���ƍl����
���̂悤�ȁ�����������Ȃ�z�����ԂƌĂ�
���[���ɏ]���Đ����ā����Ȃ���ԂɈڍs����菇�����̏�Ԃ̉��ƌĂ�
���[���ɉ����Đ�A����菜����B,C��lj��������A��A��B,C�ɕ����ƕ\������Ƃ���
�����Ԃ����������A���̉��ɂ����čŏI��ԂɎ���܂ŁA�e�i�q�_�ōs��ꂽ����̉��i�q�_���ɑ������킹�����X�g���s��ƌĂ�
(��)
�����@�����@�����@�������@������
�����@�����@�����@�������@������
�����@�����@�����@�������@�������@
�ɂ����ĉs���
�O�O�O
�P�P�O
�P�P�O
�ł���(�K�v�ɉ����čs��̃T�C�Y�͕ύX�����)
��������̉s�^����ꂽ�Ƃ��ʂ̉����\�����邽�߂Ɏ��̉������[���Ő��������l����
�����
>>622 ����
SyberMath
>>653 �f���炵��
�����ł�
����ς�ӎg�������Ȃ�܂���
�ʂɃs�b�^�����ɂȂ�Ȃ��Ă�������ł���
���̗p�ӂ�����
V(a,b)
= ��^((3min{max{0,a},max{0,b}}-|a|-|b|)/4)
�ł���
���l�^�̓E�C���N���[�́gPegs on the Half-plane�h
�������͏����̃y�O��y��0�S�̂ł��̏ꍇ�͂�������E�̗��_�l���v�Z�@�Ō��������܂Ō������Ă�Ƃ����b���ǂ����ŕ������L��������܂�(8�i�ڂ��炢���������ȁH)
���̂͂ǂ��܂ł������ł��傤�˂��H
���A����
SyberMath
����
����
>>650-652 ���̖����悭�ǂ�ŁB627�Ŗ���Ă���ŏ��̖���
�������������@
�������������@
�������������@
�ł��邪�A����͌����ʂŕ��ʂɉ�����B
�����āA���̖��Ŗ���Ă���̂�
�������������@
�������������@
������������
�ł����āA������͌����ʂɂ���@�������ɒ���ĂȂ��A�Ƃ������ƁB
>>661 ���H�����ʂʼn�����́H
�ǂ����������ʐݒ肷��́H
>>661 ���������ĔS�y�Ŕ����̂�H
���ꂨ�������Ȃ��H
���̔S�y��1
y��2�̑��|�e���V����������1�A������y=1,x��2��0.125��y=0,x��3��0.25��������Ƒ��|�e���V������1.375�Ō���1���y�������Ă��܂�
�����炻������0��x��2, 0��y��1�̏ꍇ�ł���|�e���V�����_�@�����ł͉����Ȃ��Ǝv������
>>663 �����Ă݂��������
�ł��̔z�u��������ƍl�@���邾���Ō������C������
�܂����ꂾ�Ɓu
>>650-652 �ł��悢�v�Ƃ������ƂɂȂ邪�A�ǂ݂̂��{���
�������������@
�������������@
������������
�̕��ł����āA������́u�����ʁ{�̔z�u�̍l�@�v�ł����������Ȃ�
>>664 �����
��������ƍl���Ă݂�
�ꉞ�A���Ƃ��Ƃ�
>>664 �ł���
----
����s�ʼn�������Ɖ���
�����������@�����������@�����������@
�����������@�����������@�����������@(��y=0����苎���ĉ�����)
�����������@�����������@
������(0,0),(1,0),(2,0)�̐�A,B,C�Ƃ���
�����ʼn������[���ɉ����Ď��̃��[����lj�����
--- �D��q�����[�� ---
�ړ��\�Ȑ���������ꍇC�̎q���AB�̎q���AA�̎q���̗D�揇�ʂňړ�����
���̃��[�����ł��ړ��s�\��Ԃɓ��B����ΐ͋��c��s�\�_�ɂ͎c��Ȃ����Ƃ��킩��
������C,B�̎q�����S�Ĉړ��s�\�ɂȂ�����̎����l�����
����������
����������
�̏�ԂɂȂ��Ă���
���̏�Ԃ���A�����c��s�\�_�Ɏc�炸���邽�߂ɂ�B,C�̎q����(1,1),(2,0)�Ɏc���Ă��邱�Ƃ͂ł��Ȃ�
�����B,C�̎q���̈ړ���
����������
�����������@
�����������@
�̉��łȂ���Ȃ�Ȃ�
�����_�@��p����C�̎q���ɂ��Ă�
����������
�����������@
�����������@
�̉��łȂ���Ȃ�Ȃ�
�R����x��2�̕��������̖��Ɠ����`�ł��邪�A���ɉ����ĉs��͏������Ȃ��Ă���̂Ō��̖����^�ɐ������������Ȃ��Ă��邩�疵��
>>667 ���[�ށB���ꂪ�������̂������ɂ͔��f�ł��A
���ɐ������Ƃ��Ă��A�g���Ă��錸���ʂ́u�s��v�ł����āA
�}�X���Ƃɏd����t�^����悤�ȁA������ʏ�̌����ʂł͂Ȃ��ł���
�ŁA�s��̌������ɉ�A������̂͗L���I�[�g�}�g���I�ȕ��@�ł����āA����
���R����x��2�̕��������̖��Ɠ����`�ł��邪�A
�̕������܂������L���I�[�g�}�g���I�ł����āA���ǂ���́A
���Č�������Grundy���̕��@�Ɩ{���I�ɓ����Ȃ�Ȃ������Ă���
>>668 ����Grundy�����g����@�Ƃ͂ǂ�Ȃ�ł����H
>>669 ���́A�{����Grundy�����������͊o���ĂȂ�
������ۂ������́u�Z�Z���v���g����@������
�ł�Grundy���ō����Ă��C�͂���
�ߋ����O�ɂ���͂������A������ƌ�₪�������ĒT���Ȃ�
�o�܂Ƃ��ẮA
>>627 �̖�肪�������܂ꂽ�̂��u�ʔ�����肨�����ā`�� �\�O��ځv�ŁA
Grundy��(�H)���g������@���������܂ꂽ�̂͑啪���Ƃ̂͂��ŁA
���ꂪ�ǂ̃^�C�~���O���������S���o���ĂȂ��̂ŁA�����̂Ƃ������肪�Ȃ��B
�Ȃ̂ŁA�T���Ȃ獡�܂ł̉ߋ����O��S���T�������Ȃ��E�E�E
�Ƃ������A�����`�����S���ʂ̃X���������\�����Ȃ��͂Ȃ��E�E�E
>>670 �R�����ȁH
https://algo-logic.info/combinatorial-games/#: ~:text=Grundy%E6%95%B0(Nim%E6%95%B0%2FNimber,%E3%81%A7%E3%81%8D%E3%82%8B%E3%82%88%E3%81%86%E3%81%AB%E3%81%AA%E3%82%8A%E3%81%BE%E3%81%99%E3%80%82
���̎�̖��ŕK���ł�����̓I�Ȃ��Ə����Ă��邯�ǂ��̖��Ɋւ��Ăǂ����������͈�ʘ_����͂܂�ł킩��Ȃ���
������
�u�ʔ�����肨�����ā`�� 25��ځv�܂ł������Ǝ��ƂŖڂ�ʂ��Ă݂����A
�u�ʔ�����肨�����ā`�� �\����ځv�Ŏ��̖�肪������Ă����B
891 �F�P�R�Q�l�ڂ̑f������F2011/10/24(��) 16:41:46.46
���W���ʏ�̌��_(0,0)�ɋ1�u����Ă���B
(a,b)�ɒu����Ă�������菜���A(a,b+1)��(a+1,b)�ɋ��1���u���Ƃ���������l����B
�������A(a,b+1)��(a+1,b)�̂ǂ���ɂ���u����Ă��Ȃ��ꍇ�̂݉\�Ƃ���B
���̑�����J��Ԃ��s�����Ƃ���A(0,0),(0,1),(1,0),(1,1)�̂ǂ̓_�ɂ��������ԂɂȂ����B
���̎��A(0,2),(1,2),(2,0),(2,1)��4�_�S�Ăɋ�u����Ă��邱�Ƃ��ؖ�����B
�����̂Ƃ���A
>>627 �̍Ō�ɏ�����Ă������������ɋ������ɂȂ��Ă���B
�ŁA����͓̉����u�ʔ�����肨�����ā`�� �\����ځv�̒��Œ���Ă��āA
�����͉s��Ɠ�������(�X���̒��ł͉}�ƌĂ�Ă���)���g���Ă����B
�̏���������A�����̋L���̒��ɂ������炠��f���Ɖ��ƂȂ���v���Ă���̂ŁA
�����āA�}�X���Ƃɏd����t�^����悤�ȁA������ʏ�̌����ʂɂ���
�����ɑ��݂��Ȃ��̂��m����ۂ��āA���ۂɁu�ʔ�����肨�����ā`�� �\����ځv�̒��ł��A
�����ł̏o��҂�
967 �F891�F2011/10/30(��) 00:39:47.72
>>965 ����{�œǂ�肪���l�^�Ȃ�ł����A���̖���
�u3�~3�̗̈悩����ǂ��o�����Ƃ��ł��Ȃ��v���Ƃ��������̂ŁA
��
>>927 �̍l������p�������̂ł����B
����ɋ������_�����߂Ă݂��Ƃ���A
>>891 �̖�肪�ł��܂����B
>>927 �̍l������m���Ă�l�́A�t�ɔY�܂ꂽ��������܂���ˁB
�Əq�ׂĂ���B�����ł́u927�̍l�����v�Ƃ́A
�����镁�ʂ̌�����(�s�ϗʁE�|�e���V�����E�G�l���M�[�Ƃ��Ă��)
���g������@�̂��Ƃ��w���Ă��āA���Ȃ��Ƃ������ł̏o��҂́A
���̂悤�Ȏ�@�ɂ��������ĂȂ����ƂɂȂ�B
�Ȃ̂ŁA����ł̂܂Ƃ߂Ƃ��ẮA
�E �s��(or�})���g���Ή�����
�E �����镁�ʂ́u�G�l���M�[�I�Ȏ�@�v�ɂ���@�́A��͂荡�̂Ƃ���Ȃ�
�Ƃ������������B
>>675 �܂�������
����������
����������
����������
�����Ȃ��Ȃ̂ł��Ƃ�
����������
����������
����������
�����Ȃ����m�F���邾�����
��������
����������
����������
����������
�ɓ����ăR�������Ȃ��͊��o
�Ȃ̂�
❇︎❇︎����
����❇︎��
����❇︎��
�ł�❇︎�͑S�����c��
����
�ʔŏo�Ă����
n��̐����Ƃ���
>>672 �q���g
���߂� n �͐��̋����S��
>>672 n=7�ōŏ�����ƂȂ肤��̂�P(2),P(5)���悢�����łǂ����II�^�ł����P(3),P(4)�͂悢�����ł����Ă͂Ȃ�Ȃ�
>>681 �w�`�`�Ɏ��ւ�����̂Łx�̕������M���b�v�ȋC������Ȃ�
�ŏ������n�Ƃ������A�Ⴆ����a�ɂ���
P(a)��[1,1,0,-1,-1]�̃p�^�[���������Ƃ��Ă��AP(a)�t�߂̃^�C�����O�����ۂ�
����������
����������
�̂悤�ɂȂ��Ă�Ƃ͌���Ȃ��Ǝv�����ǂǂ����낤
���݂����ȃp�^�[���̉\��������C������
�c�c�c�c�c
����������
����������
����������
����������
>>683 P(a) = a + [1,1,0,-1,-1]�Ƃ�����Ԃ͂Ƃ�����P(a)�ɂ�镪���̋��E�W����
[0,1]�~{a+1}��[1,2]�~{a+1}��[2,3]�~{a}��[3,4]�~{a-1}��[4,5]�~{a-1}
��(...�ő�l�̏c����...)
�Ƃ��������咣���Ă���̂ł��̎��_�܂ł̎咣���������Ȃ���ւ�����͂�
����������
����������
����������
����������
�̉��w����x���̏ꍇ
P(1) = 1 + [1,1,0,-1,-1] (�S�d�S��y��1�́g���h�̂݁A�悢����)
P(2) = 2 + [ 0,0,-1,0,1] ((�S�d�S��y��2�́g���h�Ɓg���h�A�悢�����łȂ�)
P(3) = 3 + [ -1,-1,1,1,0] ((�S�d�S��y��3�́g���h,�g���h,"��"�A�悢�����łȂ�)
�悢�����łȂ����̂͂����������Ƃ�������܂�
����͑���ɂ��ĂȂ�
>>684 ���[�[��肽�����Ƃ��킩�������A�Ⴆ����
�c�c�c�c�c(�����s)
����������
����������
����������
����������
�c�c�c�c�c(��s)
�̂悤��[1,1,0,-1,-1]�^���o�������ꍇ�AP(a)��艺�̗̈�����̂܂܂ɂ��ď�̗̈��
����������
����������
�c�c�c�c�c(��s)
�̂悤�ɂ��Ă�菬�������Ⴊ������Ă��Ƃ��A�Ȃ�ق�
P(a)�����[����o�����ēr���Ł��̕����ɐi�܂Ȃ����ƂƂ��͖��炩�����������A�����I�i�Ƃ�����艽��肨���l�c�j
�z����͂���Ȋ���
>>679 LHS
=��( (n_k/1_k (-1))^k )^x^k
= 2F1(-n,-n,1,1+x)
= 2F1(-n,n+1,1,(x+1)/x)(-x)^n
(�� Pfaff's transform )
RHS
= �� ( (-n)_k/1_k (-1)^k) (n+1)_k/1_k x^n/x^k
= 2F1(-n,n+1,1,-1/x)x^n
�����
2F1(-n,n+1,1,t)=2F1(-n,n+1,1,1-t)(-1)^n
�������Ώ\��
���Ӌ���ODE
t(1-t)u''+(1-2t)u' +n(n+1)u = 0
�̉��ł���
t=1�ɂ����č��ӂ͖��炩��1�A�E�ӂ�
(1-(n+1))_n/1_n(-1)^n = 1
t=1�ɂ����č���'��-n(n+1)/1�A�E��'��
n(n+1)(1-(n+1))_(n-1)/2_(n-1)(-1)^n = -n(n+1)
�œ���������ODE�̉��̈�Ӑ��ɂ��咣�͐��藧��
t=0�ɂ����Ă�����
>>687 �����ł��B���߂łƂ��������܂��B
���̖��͕̉��������āA�p�ӂ��Ă�����1���Љ�܂��B
f(t) = (1/n!) (d/dt)^n (t^n (1+t)^n)
���ʂ�ŕ]������
(1)���C�v�j�b�c���[���œW�J
f(t) = (1/n!)��[k=0,n] C[n,k] ((d/dt)^k t^n) ((d/dt)^(n-k) (1+t)^n)
= ��[k=0,n] C[n,k] n(n-1)...(n-k+1) t^(n-k) n(n-1)...(k+1) (1+t)^k / n!
= ��[k=0,n] C[n,k]^2 t^(n-k) (1+t)^k
(2)���ʂ̓W�J
f(t) = (1/n!) (d/dt)^n ��[k=0,n] C[n,k] t^(n+k)
= ��[k=0,n] C[n,k] (n+k)(n+k-1)...(k+1) t^k / n!
= ��[k=0,n] C[n,k] C[n+k,k] t^k
�䂦��
��[k=0,n] C[n,k]^2 t^(n-k) (1+t)^k = ��[k=0,n] C[n,k] C[n+k,k] t^k
�����藧�� 1/t=x�ƒu�����ƂŖړI�̌��ʂ�������
20���I�œ��炵��
>>690 ���łȂ̂ŃR�����\���Ƃ�
2009 IMO �h�C�c���
a(1),a(2),⋯,a(n) �𑊈قȂ鐳�̐����Ƃ��AM �� n-1�̐��̐�������Ȃ�W����
����B�܂��AM �� s=a(1)+a(2)+⋯+a(n) ���܂܂Ȃ��B�������� 0 �̒n�_�ɂ���o�b�^��
�������̐��̌����� n ��W�����v����B n ��̃W�����v�̋����� a(1),a(2),⋯,a(n) �̕��בւ��ł���B���̂Ƃ����בւ������܂��I�ׂA�o�b�^��M �̗v�f�ɑΉ�����n-1�_�Ɉ�x�����n���Ȃ��悤�ɂł��邱�Ƃ��ؖ�����B
�����҂̏��Ȃ�3�₾����
���Q��
https://manabitimes.jp/math/956 >>690 ��
>>678 ���f���i�ł���Ď��ɂ����ɐh��
������ł�
>>693 �ȉ����R��n�ɑ��ă�n=2��/n�A��n=exp(i��n)�Acn=cos(��n)�Asn=sin(��n)�Ƃ���
��(n)��n��4�̍ŏ����{���Ƃ���
���@n�����R���Ƃ��Al = ��(n)�Ƃ���Ƃ�Q(��l) = Q(sn,i)�ł���
[ Q(��l) : Q(sn) ] = 4 ( n �� 4 ( mod 8 ) , n��4 )
. = 2 ( otherwise )
�ł���
(��) (a) n �� 0 ( mod 4) �̂Ƃ�
Q(sn)��sn,cn���܂ނ���Q(sn,i)�̓�l���܂�[Q(��l):Q(sn)]�͍��X2�ł���
������(sn)�͋����ł����l���܂߂Ȃ��̂ł��傤��2�ł���
(b) n �� 1,3 ( mod 4) �̂Ƃ�
Q(sn)��c_n���܂�(��sin(�Ɓ~[(n�}1)/4]2∓1) = c_n)����Q(sn,i)�̓�n���܂ނƂ킩��
��l �̓�n^k�̂����ł�i�ɋ߂����̂�p����i/��n^k�Ɉ�v���邩���̋t���Ɉ�v���邩�Ȃ̂Ń�l��Q(sn,i)�Ɋ܂܂��
�����[Q(��l):Q(sn)]�͍��X2�ł���
������(sn)�͋����ł����l���܂߂Ȃ��̂ł��傤��2�ł���
(c) n �� 2 ( mod 4 ), n��4�̂Ƃ�
Q(sn,cn,i)�̓�l���܂ނ���[Q(��l):Q(sn)]�͍��X4�ł���
������Gal(Q(��l)/Q)��4�̌�
�ā��āA�ā�1/�āA�ā�-�āA�ā�-1/��
�͑S��sn=(��-1/��)/(2��^(n/4))�����Ȃ�����[Q(��l):Q(sn)]�͏��Ȃ��Ƃ�4�ł��遠
���@n�����R���Am�����̖Ƃ���Ƃ�Q(sm) = Q(sn)�ƂȂ�̂�
�藝�@�����p�`�ň�ӂ̒����ƑΊp���̒����̔䂪�L�����ƂȂ�̂͐��Z�p�`�̍Œ��Ίp���̏ꍇ�Ɍ���
>>694-696 �������������肪�Ƃ��������܂��I�I
������ ���������肪�Ƃ�
Q(sin(2��/n))=Q(sin(2��/m))
�̏����̈�Ƃ���(m,n)=(4,12)���o�Ă��āA���ꂪ���Z�p�ɑΉ�����Ƃ����̂͂ƂĂ��ʔ����ł�
�_���ɂ��Ăق������x����
��s�����݂����Ȃ̂͂���̂��ȁH
���{�̂���
>>693 �̗p�ӂ��Ă�����@���ڂ��܂�
p����f���Ƃ���p�p�`�ōl����
�Ώ̐�����2��k��p/2�������R��k�ɑ���
L=sin(k��/p)/sin(��/p)�̖������������Ώ\��
(k-1)�����`�F�r�V�F�t������U��p����
L=U(cos(��/p))�Ə�����
�����L���L�����Ȃ�Acos(��/p)�͗L�����W����(k-1)���������̍��ƂȂ邪�A
[Q(cos(��/p)):Q]=��(2p)/2=(p-1)/2��k-1
��薵��
�y���߂Ă��炦�Ă悩������ł��������Ԃ��Ƃ�����Ƌc�_�ɃW�����v������̂ō����ւ��܂�
���̎�̘b�ǂ̂��炢��s���������邩�悭�͒m��܂��~���̂̃K���A�Q�̍�p�͎��ʂقǒ��ׂ��Ă�Ǝv���܂�
�咣���Y�킾�������`�����ǂ����̃n�Q�^�J�G���Ɍf�ڏo���Ȃ����ȁH
130km/h�ő�����20�������鋗����100km/h�ő���Ɖ���������܂����H
������蔼������
>>705 ���肪�Ƃ��������܂����B
P(x)�f���W���̑������Ƃ���
�������⎗�����k^5/(e^2��k-1)�݂����Ȃ̂Ȃ������H
http://2chb.net/r/livejupiter/1648270223 ���
0001 ������������ 2022/03/26 13:50:23
4✖1/8✖3/4����3/8�ɂȂ�́H
4��1/8�Ŗo�����ȁH����Ƃ�1/8��������4��3/4��3/1�ɂȂ��H
>>710 f(z) = P(z^4) z^5 ��/(sinh(��z)sin(��z)) �̋ɂ̈ʒu�Ƃ��̗����ׂ�
��H
�����̖���\��܂�
��(1/4)�Ƃ��o�Ă���悤��
>>715 ��(1/4)�͏o�Ă��Ȃ�
�̒��z���݂̂ł�����
>>712 �悭�l�����炱�̉A�s��������Ǝv��
�����sinh(��x)�̃��ΈȊO�̐��̐��ł悢���ƂɂȂ邪����͂�������
�������͑��0�ł͂Ȃ�
f(i),f(2i),f(3i),...���ɂŃA�[�x���v���i�o����Ƃ��̋�����̐ϕ������U�ϕ��ɂȂ�̂�
�ɂ𒆐S�Ƃ��鏬���~�����H���悯�ė����̔����̒l��]������K�v������
>>715 �ł��萔���̐ϕ��ɂ͏o�Ă����ˁH
�萔���ȊO�͑S�������l�ɂȂ��Ȃ��́H
�ɂ̂Ƃ��낿����Ƃ悯�������Ȃ���
>>719 �Ȃ��H
f(iy)-f(-iy)�~��ϕ�����ˁH
���~��ł��ꎩ�̂������������ĂȂ��H
�Ȃ��Ⴂ���Ă邩��
���A�z���g��
���A������
>>720 �A�[�x���v���i��wikipedia�̏ؖ�(f(z)�͋���ŋ�����ɋɂ�����Ɖ���)
https://en.wikipedia.org/wiki/Abel%E2%80%93Plana_formula ��a=i+�Á�i+0�ŋɌ������Ƃ��̔�ϕ��������
a f(at)��i f((i+0)t)�͋����̉E�����E��ϕ���
a^(-1)f(a^(-1)t)��-i f((-i+0)t)=-i f((i-0)t)�͋����̍������E���t�����ɐϕ�����
����������f(z)�̗������o��
�����
>>703 (130/100)�~20=26(��)
>>712 �̉̏C���ł��ȉ��Ɏc���Ă����܂��B
k��5, k��1(mod 4)�ɑ���
������̗���������A�[�x���v���i�̌������
I = �� n^k/sinh(��n)
= ��[0,��] x^k/sinh(��x)dx - 2��(-1)^n n^k/(e^(2��n)-1)
J = ��(2n)^k/sinh(2��n)
= ��[0,��](2x)^k/sinh(2��x)dx - ��(-1)^n n^k/(e^(��n)-1)
2J-I = ��(-1)^n n^k/sinh(��n)
= 2��(-1)^n n^k(1/(e^(2��n)-1)-1/(e^(��n)-1))
= -��(-1)^n n^k/sinh(��n)
= -(2J-I)
����������
2J-I = 0
>>707 �̗p�ӂ��Ă����͈ȉ��̒ʂ�ł��B
f(z) = P(z^4) z^5 ��/(sinh(��z)sin(��z))�ƒu��
f(z)�̋ɂ�z=n, in�ɂ���(n��0�łȂ�����)������
Res[z=n]f(z) = Res[z=in]f(z) = (-1)^n P(n^4) n^5 / sinh(��n)
���������ė����藝���
4��[n=1,N] (-1)^n P(n^4) n^5 / sinh(��n) = 1/(2��i)��[C]f(z)dz
������C�͓_(1+i)(N+1/2),(1-i)(N+1/2),(-1-i)(N+1/2),(1-i)(N+1/2)������H
n�����Ƃ����|��[C]f(z)dz| = O(N^(4+deg(P))/e^(��N)) �� 0
���ړI�̌��ʂ�������
>>726 ����H
����2J-I = -(2J-I)�ɂȂ��H
�I���v�Z������2J-I = 2J-I�ŐU��o���ɖ߂��ă_���������C���������
>>726 ���̌v�Z�ق�Ƃ�k��1(mod4)�g���Ă�H
�����f���ɗ������܂Ƃߒ�����2J-I = 2J-I�ɖ߂��Ă��܂�
k��1(mod4)�Ȃ�܂Ƃߕ��M����2J-I = -(2J-I)�ɂ��ǂ蒅����̂�������Ȃ�����
���Ȃ��Ƃ����̏����Ȃ��ł͔��Ε����ɍs�������͂��Ȃ��Ǝv���A���̏����Ȃ��ꍇ�ɂ͂����������l�����I�ɂO�ɂȂ�Ȃ��̂͊m��I������
>>272 k=5,k=9�Ɋւ��Đ��l�I�Ɋm�F�����Ƃ���
>>726 ��I��J�̐ϕ��Ƙa�̎��͍����Ă�
�a��L���ɂ���2J-I�̎��𐔒l�I�Ɋm�F�������ǖ��Ȃ�����
>>729 �z���g�H
����ǂ���k��1(mod4)�g������H
��������܂Ƃߒ�����Ƃ͂Ȃ�Ȃ�k�������ł��s�������ł��Ęa�̓�[n]n^k(q^(2n)-1)�̌`�ɂȂ��ċ����������E���グ������[n]n^k(q^(n)-1)�̌`�ɂ͂Ȃ�(�R�b�`�͗������O�łȂ��_���������ɂȂ���/(q^2n-1)�̘a��/(q^n-1)�̘a�ɂȂ�
�������̕�2�{������ʂ������������ɂȂ��Ăđł����������Ĉ����Z�����Ƃ����ꂢ��q^n(q^n-1)�ɂȂ��ċ������������Ă���q^n-1�̕����Y��ɏ����Ă����q^n/(q^(2n)-1)�ɂȂ��Ă��Ƃ�sinh(x)�ɖ߂�Ƃ��܂Ŋm�F���āu���A�ł������H�v�Ǝv�������ǂ悭�悭�l�����炻��Ȃ͂��Ȃ��A���������ǂ��ɂ�k��1(mod4)�g���ĂȂ��A�g�킸�ɂł���͂��Ȃ��Ǝv���ČW��������U��o���ɖ߂��Ă������ƋC�Â����܂ł�����̐Q��O����������
����������ĂȂ��H
>>730 f(x) = x^k/sinh(��x)
�ƒu����
Res[x=ni]f(x)/(e^(-2��ix)-1)
= ((ni)^k/((-1)^n))/(e^(2��n)-1)
������k��1(mod4)�̎�
= i (-1)^n n^k/(e^(2��n)-1)
>>731 �C���ʂ�k��1(mod4)�ł��낤���Ȃ��낤�����������_�ɈႢ�͏o�Ȃ��ł���
���ꂪ�O�ɂȂ�̂�sinh(��x)�ł��ꂪ�O�ɂȂ�̂�x=mi�ƂȂ�Ƃ��ł��鎖��k�̒l�͊W�Ȃ�
�ŁA���̎���x�̒l�ł���mi��x^k/(e^(2��x-1)�ɑ�����鎖��k�̒l���Ȃ�Ȃ�����ł��x��Ȃ�����o����
���ꂾ���ł͌��ɖ߂�Ȃ����ǁA���2�~�������݂̂ɂ����������ł���̂�k��1(mod4)�o�Ȃ��Ă��o����ł���H
>>731 1/���Y�ꂽ�̂Œ���
Res[x=ni]f(x)/(e^(-2��ix)-1)
= ((ni)^k/(��(-1)^n))/(e^(2��n)-1)
������k��1(mod4)�̎�
= (i/��) (-1)^n n^k/(e^(2��n)-1)
�ȂM�����Ȃ��Ȃ�
>>733 ������x^k��x=mi���������
m^k i^k �ɂȂ邩�� i=i^k�����藧������k��1(mod4)
����ƍ���̃m�[�g������
>>735 �C���A�ǂ������Ƃ�����k��1(mod4)�łȂ��ꍇ�͌��ɖ߂��ĈӖ��̂Ȃ����ɂȂ�A�Ȃ���k��1(mod4)�̂Ƃ��������ɖ߂炸�a���O�ɂȂ�ؖ��ɂȂ�Ƃ������ۂ��N���������ɂȂ�
�������ƕ����Ă邯�ǂ���Ȃ̌������ƂȂ���
�����Ɗ�ŕБ������O�ɂȂ�Ȃ���〜�͂��邯�ǂ�
> �C���A�ǂ������Ƃ�����k��1(mod4)�łȂ��ꍇ�͌��ɖ߂��ĈӖ��̂Ȃ����ɂȂ�A�Ȃ���k��1(mod4)�̂Ƃ��������ɖ߂炸�a���O�ɂȂ�ؖ��ɂȂ�Ƃ������ۂ��N���������ɂȂ�
���悤�ł���
�Ƃ���ǂ���~�X�����邩��K���ɏC�����Ă�������
>>739 �̒���
��n^k/(e^(2��n)-1) = (1/2) B[k+1] / (k+1)
������k=5,9,13,�c��B[n]�̓x���k�[�C��
���̎��͂悭�m���Ă���Wolfram�̃f�[�^�x�[�X�ɂ���
>>726 �̑z���
�~ n�����Ƃ����|��[C]f(z)dz| = O(N^(4+deg(P))/e^(��N)) �� 0
�Z N�����Ƃ����|��[C]f(z)dz| = O(N^(6+deg(P))/e^(��N)) �� 0
�ł͂��₷�݂Ȃ���
>>726 �̕⊮�A��ӐQ�ė�Âɍl�������NJԈႢ��������Ȃ��B
Wolfram�搶���������炵���ƌ����Ă���̂ł����A�Ȃ��Ⴂ���Ă�����w�E���肢���܂��B
�ȉ�Wolfram�ł̌��Fk=5�ɌŒ�
I�̎�
https://www.wolframalpha.com/input?i=%CE%A3%5Bn%3D1%2C%E2%88%9E%5D+n%5E5%2Fsinh%28%CF%80n%29& ;lang=ja
��[n=1,��] n^5/sinh(��n)
�� 0.253522
https://www.wolframalpha.com/input?i=%E2%88%AB%5B0%2C%E2%88%9E%5D+x%5E5%2Fsinh%28%CF%80x%29dx& ;lang=ja
https://www.wolframalpha.com/input?i=%CE%A3%5Bn%3D1%2C%E2%88%9E%5D+%28-1%29%5En+n%5E5%2F%28e%5E%282%CF%80n%29-1%29& ;lang=ja
��[0,��] x^5/sinh(��x)dx - 2��[n=1,��] (-1)^n n^5/(e^(2��n)-1)
�� 0.25 - 2*(-0.00176091)
�� 0.25352182
�Ő��l�I�ɂ͐������炵��
J�̎�
��[n=1,��] (2n)^5/sinh(2��n)
�� 0.126761
��[0,��](2x)^5/sinh(2��x)dx - ��[n=1,��] (-1)^n n^5/(e^(��n)-1)
�� 0.125 - (-0.00176091)
�� 0.12676091
�ł�������������炵��
�Ō��2J-I�̉E�ӂƍ��ӂ̘a�̍��̕����̃`�F�b�N
�a�̑S���ׂ�͖̂ʓ|�Ȃ̂ŁA�����Ƒ�ׂ݂̂�
2J-I����(��`��)��2��=2(J�̏���)-(I�̏����Ƒ��)
�� 2*((2*1)^5/sinh(2��*1))-(1^5/sinh(��*1)+2^5/sinh(��*2))
�� 0.03292721409509456116
2J-I�E��(�A�[�x���v���i)��2��=2J-I�̐ϕ����Ȃ����a�̏����Ƒ��
-2((-1)^1 1^5/(e^(��*1)-1)+(-1)^2 2^5/(e^(��*2)-1))
+ 2((-1)^1 1^5/(e^(2��*1)-1) + (-1)^2 2^5/(e^(2��*2)-1))
�� -0.03292721409509456116
�ʼnE�ӂƍ��ӂ̍��̕��������傤�Njt�ɂȂ��Ă��Ė��Ȃ�����
���܂�A�I��������Ԉ���Ă�
�m�F���肪�Ƃ�
�Ƃ����
>>741 �̓���
> ��n^k/(e^(2��n)-1) = (1/2) B[k+1] / (k+1)
> ������k=5,9,13,�c��B[n]�̓x���k�[�C��
��Wolfram�̃T�C�g�Ȃǂ��������Ă��o�Ă��Ȃ��悤��
�悭�m���Ă���Ƃ����̂͊��Ⴂ�������悤�ł��A���܂Ȃ�
�����Ȃ�̏ؖ��͂ł��Ă��邯�ǂ�����Ƃ������������������Ă��o�Ă��Ȃ��̂�
�N���o�T��m���Ă����狳���Ăق���
���邢�͂��̓������ؖ����Ă���Ă����\�ł�
>>691 a(1)<...<a(n)�Ƃ��Ă悢
M={m(1),...m(n-1)},
m(1)<...<m(n-1)�Ƃ��Ă悢
n�ɂ��Ă̋A�[�@
n��2�̂Ƃ��e�Ղ�����n��3�Ƃ���
(I) m(n-1)��s-a(m)�̂Ƃ�
�K�v�Ȃ�a(1)〜a(n-1)����ѕς��ċA�[�@�̉��肩��a(1),a(2),...,a(n-1)�Ɣ���m(n-1)�ȊO�̒n�_�͑S�Ă��킵��s-a(n)�n�_�Ɏ����Ƃ��Ă悢
��[k��i]a(i)��m(n-1)�ƂȂ�ŏ���k���Ƃ��(�扼�肩�班�Ȃ��Ƃ�i=n-1�Ő�������̂ŕK�����݂���)
��[k��i]a(i)=p�A��[k��i]a(i)=q�Ƃ���p<m(n-1)��q�Aq-p=a(k)<a(n)�ł��邩��p<m(n)<p+a(n)�ł���
�����a(1),a(2),...,a(k-1),a(n),a(k),..,a(n-1)�Ɣ�ׂΑS�Ă̋֎~�n�_�����킹��
(ii) s-m(n) < m(n-1) < s�A����s-a(n)���֎~�n�_�łȂ��Ƃ�
(ii)�Ɠ������K�v�Ȃ�a(1)〜a(n-1)����ѕς��ċA�[�@�̉��肩��a(1),a(2),...,a(n-1)�Ɣ���m(n-1)�ȊO�̒n�_�͑S�Ă��킵��s-a(n)�n�_�Ɏ����Ƃ��Ă悢
���̏ꍇ��s-a(n)�̒n�_����s�֔�ׂ͂悢
(iii) s-m(n) < m(n-1) < s�A����s-a(n)���֎~�n�_�̂Ƃ�
s-a(m) = m(k)�Ƃ���
���̎�����l��s-a(l)��s-a(l)-a(m)�̂�������֎~�n�_�łȂ�l��[1,n-1]���Ƃ��A�Ȃ��Ȃ炻���łȂ��Ƃ���ƑS�Ă�l��[1,n-1]��s-a(l)��s-a(l)-a(m)�̂����ꂩ�ЂƂ��K���֎~�n�_�ƂȂ�A�����̒n�_�͑S�đ��قȂ邩�炱���n-1�̋֎~�_�S�Ă��s������Ȃ���Ȃ�Ȃ����A���̒���s-a(n)�͊܂܂�Ȃ��̂ʼn���ɔ����Ă��܂�
�A�[�@�̉��肩��a(l)��a(n)�ȊO��n-2��̃W�����v����בւ���m(n-1)��m(k)�ȊO�̑S�Ă̋֎~�n�_�����킵��s-a(l)-a(n)�̒n�_�܂œ��B�o����
��������a(n)�Aa(l)�Ɣ�ׂΒlj�����钅�n�n�_��s-a(l)�����������������
>>707 ���ꓖ�R�ȉ~���_�̉�����Ǝv���Đ}�����Œ��ׂĂ����炠����
Jacobi��
Fundamenta Nova Theoriae Functionum Ellipticarum
�ɂ����ς������ڂ��Ă�
�ǂ�ł悭�킩����
���}�k�W������notebook�ɂ��������������ς��ڂ��Ă邯�Ǒ�{�͂��̃��R�r�̗��_�Ȃ���
���̖{�Ɂu�ڍׂ͏Ȃ����ǂ��̒��q�ŔC�ӂ̎��R���ɑ��Čv�Z����A���S���Y�����Ƃ��v�Ƃ����̂����ۂɂ���Ă݂Ă�̂����}�k�W������notebook�̌v�Z�ȂƉ��߂Ēm����
�������R�r�̎��ォ���{�A���S���Y���͊m�����Ă�����
------
�m�[����q=exp(−��K��/K)�Ƃ��A������v=��u/(2K) �ƕϊ�����B���̂Ƃ�
sn^2(u)
= 4K^2/��^2-4KE^I/��^2
- 8 ��lq^l/(1-q^(2l)) cos(2lv)
�ł��邩��
sn(K-u)^2
= 4K^2/��^2-4KE^I/��^2
- 8 ��lq^l/(1-q^(2l))(-1)^l cos(2lv)
�ł���j��1�ɑ���v�̊��Ƃ��Ă�2j����maclaurin expansion�̌W����
-8(-1)^j2^(2j)/(2j)! �� l^(2j+1)q^(l)/(1-q^(2l))
�ł���
�����
sn^2(K-u)
= cd^2(u)
= (cn/dn)^2(u)
= (dn^2 + (-1+k^2) sn^2)/dn^2
= 1 - k��^2sd^2(u)
�ɂ��-1+sn^2(K-u)�͋���ł��肳���
-1+sn^2(K-iu)
= - k��^2sd^2(iu)
= - k��^2(sn(iu)/cn(iu))^2
= - k��^2(i sn��(u)/cn��(u) cn��(u)/dn��(u))^2
= + k��^2(sd��(u))^2
= 1 - sn��^2(K��-iu)
�ł���
����ē���k=1/2�̂Ƃ���2j �� 0 (mod 4)�̍���vanish���遠
>>746 ���炵���I���x���̕������Ă���
�Q�l�܂łɏ�ŗ��p�����ؖ��ɗ��p���������̂�����������������p109 sec.41 ��(1)��
>>744 �̏o�T���킩����
Eisenstein����
G_{2k}(��) = ��[(m,n)��(0,0)] 1/(m+n��)^(2k)
��Fourier�W�J
G_{2k}(��) = 2��(2k) + 2(2��i)^(2k)/(2k-1)! �� ��_{2k-1}(n) e^(2��in��)
��Lambert�����ɒ����ă�(2k)�̓���l��2k��2(mod 4)�̂Ƃ��̒l
G_{2k}(i) = 0
��G_{2k}(1/i) = i^(2k) G_{2k}(i)
�������邱�Ƃœ�����悤�ł�
>>744 ��k<0�̌����̋L�q�Əo�T��
���[�}���̃[�[�^���A���{�k��A���q���X pp21-22�ɂ������B
����ɂ���Ramanujan's Notebooks Part II �� Ch.14 �ɂ�����悤��
�悭�m���Ă���悤�ł��B
���ł�k��5�̎莝���̉�\���Ă����B
k��5�ȏ�̐�����k��1(mod 4)�Ƃ���
���̂Ƃ�
��[n=1,��] n^k/(e^(2��n)-1) = ��[0,��] x^k/(e^(2��x)-1) dx ---- (1)
�����藧��
��������肷���
(1)�̉E��
= ��[n=1,��]��[0,��] x^k e^(-2��nx) dx
= ��(k+1)��[n=1,��] 1/(2��n)^(k-1)
= k!��(k+1)/(2��)^(k+1)
= B_{k+1}/(2(2k+1))
�ȉ�(1)������
f(z) = z^k ��cot(��z)coth(��z),
g(z) = z^k ��coth(��z)
N�𐳂̐����Ƃ���C��_(-1-i)(N+1/2)����_(1-i)(N+1/2)�̌����̒����Ƃ���
���
1/(2��i)��[C] f(z)dz = ��[n=1,N] n^k coth(��n),
1/(2��)��[C] g(z)dz = ��[n=1,N] n^k + 2��[0,N+1/2] x^k/(e^(2��x)-1) dx - R,
R = 2im(��[0,N+1/2](N+1/2+iy)^k/(e^(2��(N+1/2+iy))-1) dy)
�����藧��
�ؖ��̊T�v��
f(z)�Ɋւ��Ă�C�����_���S�Ƀ�/2�Â�]�����������`�̕Ȑ��Őϕ���
g(z)�Ɋւ��Ă�C�Ǝ������܂ޒ����`�̕Ȑ��Őϕ����Ώ̐���p���Ċȗ�������
���̕���N�����Ƃ����
��[C]|f(z)-ig(z)||dz| = O((N+1/2)^(k+1) e^(-2��(N+1/2))) �� 0,
R = O((N+1/2)^(k+1) e^(-2��(N+1/2))) �� 0
�ł��邱�Ƃ���(1)��������
�Ƃ����킯�Ō��Ǒȉ~���̃����x���g�������������R�ɂł���悤�ɂȂ�Ȃ��Ɖ����n�܂�Ȃ�
>>751 sn(u)�ɂ���Fourier�����Ōv�Z���Ă݂�
�܂�sn(u)��u=iK',2K+iK'�ɋɂ�������4K��2iK'�̓�d�������ł��邱�Ƃɒ��ӂ���
(����͉��@�藝��Jacobi's imaginary transformation����m�F�ł���)
sn(u) = ��[n��Z] c[n] e^(i��nu/(2K))
���̌W����
c[n] = 1/(4K)��[0,4K] sn(u)e^(-i��nu/(2K)) du
�ł���
�����Ĕ�ϕ�����f(u)�ƒu��0����4K�܂ł̐ϕ���
�EC1:0����2iK'�̐���(������iK'�̋ɂ͍����̔������~�ł悯��)
�EC2:2iK'����4K+2iK'�̐���
�EC3:4K+2iK'����4K�̐���(������4K+iK'�̋ɂ͍����̔������~�ł悯��)
�̐ϕ��ɒu��������
C1��C3�̐ϕ��͎���������ł���������
c[n] = 1/(4K)��[C2]f(u)du + 2��i/(4K)(Res[u=iK']f(u)+Res[u=2K+iK']f(u))
= c[n] e^(��nK'/K) + ��i/(2kK) (1-(-1)^n)e^(��nK'/(2K))
����������
n:odd �̂Ƃ� c[n] = ��i/(kK) e^(��nK'/(2K))/(1-e^(��nK'/K))
n:even �̂Ƃ� c[n] = 0 (n=0�̎���sn(u)������ł��邱�Ƃ��琬�藧��)
�ȏ�q=e^(-��K'/K), v=��u/(2K)�ƒu���Ă܂Ƃ߂��
sn(u) = 2��/(kK)��[n=0,��] q^(n+1/2)/(1-q^(2n+1)) sin((2n+1)v)
���l�ɂ���sn(u)^(2m+1),m=1,2,..��W�J���Ă݂�
sn(u)^(2m+1) = 2��/(k^(2m+1)K)��[n=0,��] a[m,n] q^(n+1/2)/(1-q^(2n+1)) sin((2n+1)v),
a[m,n] = k^(2m+1) Res[u=iK'] sn(u)^(2m+1) e^(-i��(2n+1)(u-iK')/(2K))
= Res[u=0] e^(-i��(2n+1)u/(2K)) / sn(u)^(2m+1)
���̗�����sn(u)�̃}�N���[�����W�J�����̓I�Ɍv�Z�����
a[1,n] = (1/2)(1+k^2 - ��^2 (2n+1)^2/(2K)^2),
a[2,n] = (1/8)(3+2k^2+3k^4) - (5/12)(1+k^2)��^2 (2n+1)^2/(2K)^2 + (1/24)��^4 (2n+1)^4/(2K)^4,
...
�Ń��R�r�̋��ȏ���Sec.44 I�ƈ�v����
>>752 ������������Ă����ł���
�ׂ����v�Z�̓`�F�b�N���傤���Ȃ�
�܂��Ƀt�[���G�ϊ����v�Z����ł�
�����p�ӂ��Ă��͂Ƃ肠�����܂�sn(u)�Acn(u)�Adn(u)�̕�����������\�������߂Ă��܂��Ƃ�����n�߂܂�
�Ƃ肠����
s(x) = 2kK/�� sn( 2Kx/�� )
�Ƃ܂��K�i�����܂�
��=��/2�A��=��K'/(2K)i�Ƃ�����s(x)�͎���4���A4���̎�����
�ɂ�x = a��+b���ň�ʂ̋ɂł��藯����(-1)^(b+1)/2
�����csc(x)�̕�����������\���ɂ��
s(u) + C = ��[b:odd]( csc(x - b��) + csc( x + b�� ) )
= ��[b:odd](sin(x+b��) + sin(x-b��))
/ (sin(x+b��)sin(x-b��))
= ��[b:odd](sin(x+b��) + sin(x-b��))
/ (sin(x+b��)sin(x-b��))
= ��[b:odd]4sin(x)sin(b��))
/ (cos(2b��) - cos(2x))
= ��[b:odd]4sin(x)��q^b(1+q^b)
/ ( q^(2b) - 2q^bcos(2x) + 1)
��x=0��������C=0���o���܂�
���l�̍�Ƃ�
c(x) = 2kK/�� cn( 2Kx/�� )
d(x) = 2K/��( 2Kx/�� )
�ɑ��čs����
c(x) = ��[b:odd](-1)^((b+1)/2)4sin(x)��q^b(q^b-1)
/ ( q^(2b) - 2q^bcos(2x) + 1)
d(x) = 1 + 4��[b:odd]��(b)(q^2b-1cos(2x))
�@/ ( q^(2b) - 2q^bcos(2x) + 1)
�܂�(���Ȃ��Ƃ�sn(x),cn(x)�̓��R�r�̋��ȏ��Ɍ��ʂ��ڂ��ĂĂ���Ɠ����Ȃ̂ł����Ă�Ǝv���܂�)
�Ō��d(x)�̒萔����
��[0,K]dn(u)du
= ��[0,K](asin(sn(x))' dx
= [ asin(sn(x)) ]^K_0
= ��/2
�ŋ��߂��܂�
���̕�����������\���𗘗p����Ύ������ւ̃t�[���G�W�J���w�����̉��K���x���̐ϕ��ł�
���������̃����x���g�����߂��Ⴍ����ʔ���
�Ⴆ��s(��/2)=c(0)�ł������ꂩ��
��q/(1-q) - ��q^3/(1-q^3) + ��q^5/(1-q^5) - ...
=
��q/(1+q) + ��q^3/(1+q^3) + ��q^5/(1+q^5) - ...
�Ȃ�ł̂��o�Ă��܂����A�}�W���H�Ǝv���Ċm�F���Ă݂�Ɗm���ɐ������A����W�J����킩��܂�
���Ȃ݂ɂ���̓��R�r�̋��ȏ��́�40���炢�ōł���{�I�ȓ����Ƃ��Ă���(5)�̓����ł�
���R�r��(4)��(5)�̓��l�������W�����[�ϊ��ŏo���Ă܂����A����dn(x)�̓W�J�̒萔���̌v�Z������������Ƃ��ł���悤�ł�
�Ƃ͂������W�����[�ϊ��͂��̋��ȏ��̖ڋʒ��̖ڋʂł�����������ǂވӖ��Ȃ��ł�����
���������� c��(1,2], K>0 �͑��݂��邩�F
>>755 �q���g�@�����́w���݂���x
S(x,t) := (x+t)^c + (x-t)^c �Ƃ����ƁA
0��t��x^(c�݂̂Ɉˑ����邠��萔) �̎� |��S/��t|��(c�݂̂Ɉˑ����邠��萔) ��������̂ł��ɂ傲�ɂ�
c = 1+1/m�Ƃ���Am��3�Ƃ���
>>759 ���j�͗ǂ����������ǂ������~�X��������ۂ�
> �� (3t)^m < m^m (x-t)^(m-1)
> �� t < x^((m-1)/m) & 3��m
����\�������ɂȂ��Ă邩�˂�
�Ō�̏�������� (3t)^m < m^m x^(m-1) �܂ł��������Ȃ��C������
> ��(x+x^((m-1)/m)-1)^(1+1/m) �� 2(x+1)^(1+1/m)
> ��x + x^((m-1)/m) -1 > 2^(1/m)(x+1)
�������Ō�̉E�ӂ� 2^(m/(m+1)) (x+1) ����Ȃ����ȁ@������
> ��x��3, m��100000000
���\�������ɂȂ�Ȃ��Ă܂���
�Ƃ͌����p�����[�^���܂���������܂����������Ȃ̂ł�����Ə����D��
c = 3/2 �ŌŒ肷��Bx��9, 0��t��1+2x^(1/2) �̎�
��S/��t = (3/2)((x+t)^(1/2) - (x-t)(1/2))
= (3/2)��_[x-t,x+t] (1/2)X^(-1/2)dX
< (3/2)��_[x-t,x+t] (1/2)(x-t)^(-1/2)dX
= 3t/(2(x-t)^(1/2))
�� 3(1+2x^(1/2))/(2(x-1-2x^(1/2))^(1/2))
= 3(1+x^(-1/2))/(2(1-2x^(-1/2)-x^(-1))^(1/2))
�� 21/(2��2).
�䂦�ɁA0<K��(2��2)/21 ���� x��9 �̎��At �� 0 ���� [1+2x^(1/2)] �܂œ������Ƃ�
[KS(x,t)] �� [2Kx^(1/2)] ���� [KS(x,2x^(1/2))] �܂ł̑S�Ă̐������Ƃ�B
�i�����܂łł������������j
>>760 > �� (3t)^m < m^m (x-t)^(m-1)
> �� t < x^((m-1)/m) & 3��m
����\�������ɂȂ��Ă邩�˂�
�����������
3^m < m^m�At^m < (x-t)^(m-1)
���\�������Ƃ��ĂƂ��
��҂�
t^((m/(m-1))<x-t
��t+t^((m/(m-1)) < x
�ł����2t^((m/(m-1)) < x���\����t<(x/2)^((m-1)/m)���\��
2(x+1)^(1+1/m) < ( x+ (x/2)^((m-1)/m) )^(1+1/m)
��2^(m/(m+1)) (x+1) < x + (x/2)^((m-1)/m)
�̂��߂ɂ�2^(m/(m+1))<2�A2<(x/2)^((m-1)/m) ���\��
m=10000000�Ax��4�ŏ\��
�d
���v���Ǝv�����Ǎ��o��̃}�N�h�ŏ������̂������Ȃ�����X�}�z�̉�ʂł����ł��Ȃ�
��������ȏケ��l�߂�̂�����ǂ��̂ł���Ń_���Ȃ�s�����ł����ł�
�Ǝv�������Ǎs����킯�Ȃ���w
�Ǝv�������ǖ���
c = 5/4�Ƃ���
s'(t) = 5/4 2t/((x+t)^(3/4) + .. + (x-t)^(3/4))
< 5/2 t / (4 (x-t)^(3/4)) < 1
if 5/2 t < 4(x-t)^(3/4)
iff (5/8)^(4/3) t^(4/3) + t < x
if t < x^(3/4) and x �� 22
�� LHS mono. increase and
(5/8)^(4/3) x + x^(3/4) < x
if x^(3/4) < (1-0.535)x
iff x>(1-0.535)^(-4)
iff x > 21.388887117622...
2(x+1)^(5/4) < (x + x^3/4)^(5/4) + (x-x^3/4)^(5/4)
holds if x �� 63
(1+1/x^(1/4))^(5/4) + (1-1/x^(1/4))^(5/4) - 2*(1+1/x)^(5/4)
�v�Z�@����
c = 5/4�Ƃ���
s'(t) = 5/4 2t/((x+t)^(3/4) + .. + (x-t)^(3/4))
< 5/2 t / (4 (x-t)^(3/4))
s'(t)<1�ɂ�5/2 t < 4(x-t)^(3/4)���\���ŁA�����
(5/8)^(4/3) t^(4/3) + t < x�d�@
�ŏ\���A�����t < x^(3/4) and x �� 22�ŏ\��
( �� �@���ӂ�t�̊��Ƃ��ĒP������
�����t=x^(3/4)�Ő�������Ηǂ�
�܂�
(5/8)^(4/3) x + x^(3/4) < x
�ł���悭�A(5/8)^(4/3)=0.5343..�ɂ��x^(3/4) < (1-0.535)x�ŏ\���ł����x>21.388887117622�̎����� )
�����
2(x+1)^(5/4)
<(x+x^3/4)^(5/4)+ (x-x^3/4)^(5/4)
����������悭�A����͐��l�������x��63�Ő���
(note)
��搶�̌v�Z�ɂ��n��63�Ő�������悤�ł���
�������O���t�͔��]���Ă��̌�O�Ɏ������邪�O������邱�Ƃ͂Ȃ��悤�ł���
�܂�[63^1.25 + 63^1.25] = 354�ł���A1000�ȉ��̎��R�����\���\�ł���̂͌v�Z�@�Œ��ڊm�F�o����
https://ideone.com/UAuqsb plot ((x + x^(3/4))/(x+1))^(5/4) +((x-x^(3/4))/(x+1))^(5/4), from 62 to 63
https://www.wolframalpha.com/input?i=plot+%28%28x+%2B+x%5E%283%2F4%29%29%2F%28x%2B1%29%29%5E%285%2F4%29+%2B%28%28x-x%5E%283%2F4%29%29%2F%28x%2B1%29%29%5E%285%2F4%29%2C+from+62+to+63& ;lang=ja
�����A���܂���
>>764 �v�Z�@��M������W�b�N�͐��������������������ł�������
�����l�ł���
���Ȃ݂�
>>760 ���瑱����Όv�Z�@�̗͂��肸�Ƃ��M���\�ȃ��x����
x��9 �̎�
S(x,2x^(1/2)) > 2S(x+1,0)
iff (x+2��x)^3 + (x-2��x)^3 + 2(x^2-4x)^(3/2) > 4(x+1)^3
iff (x^2-4x)^(3/2) > x^3-6x^2+6x+2
iff (x^2-4x)^3 > (x^3-6x^2+6x+2)^2 (��x��9�͈̔͂ł͗��ӂƂ���)
iff x^3-3x^2-6x-1 > 0
�ł���A�Ō�̕s������ x��9 �ŏ�ɐ��藧���߁A
x��9 �Ȃ�� [KS(x,2x^(1/2))] �� [2K(x+1)^(3/2)] �����藧�B
�ȏ���A0<K��(2��2)/21 �Ȃ�� [KS(9,6)]=[(15��15+3��3)K] �ȏ�̐����͑S�ĕ\����B
����āAK=1/100 �Ƃ����� [(15��15+3��3)/100] = 0 �ȏ�̐�����
�S�ĕ\���邱�Ƃ�������̂ŁA�����ꂽ�B
�ق�Ƃ̓E�F�A�����O�̖��݂�����
������̂Ăł����邩������
������悤�ł�
������̂Ă��ƍň��P�[�X��x+x^3/4,x-x^3/4�̗�����1�߂���̂Ă���\�������邯�ǂ���ł�(x,x) 〜(x+x^(3/4),x-x^3/4)�܂ł�f�̑�������(x+1,x+1)〜�̃u���b�N�ɂȂ���\�������Ƃ���
2(x+1)^(5/4)
��(x+x^3/4-1)^(5/4)+ (x-x^3/4-1)^(5/4)
���Ƃ��
������x=1/t^4�ƒu������
2(1/t^4+1)^(5/4)
��(1/t^4+1/t^3-1)^(5/4)+ (1/t^4-1/t^3-1)^(5/4)
��
2(t^4+1)^(5/4)
��(1+t-t^4)^(5/4)+ (1-t-t^4)^(5/4)
��
2��((1+t-t^4)/(1+t^4))^(5/4)+ ((1-t-t^4)/(1+t^4))^(5/4)
��搶�ɂ��Ƃ����t��0.25�ł͐�������
https://www.wolframalpha.com/input?i=plot+%28%281%2Bt-t%5E4%29%2F%281%2Bt%5E4%29%29%5E%285%2F4%29%2B+%28%281-t-t%5E4%29%2F%281%2Bt%5E4%29%29%5E%285%2F4%29++from+0.24+to+0.25& ;lang=ja
���Ȃ킿x��256�ł͐�������̂�256�܂ł͌v�Z�@�Ŋm�F�������
���Ȃ킿2�~[256^5/4] = 2048�܂ŕ\���ł��邩�m�F����Ηǂ�
����͊ȒP
https://ideone.com/L4Oe7U >>768 ����A�u���b�N���q����Ȃ��S�z�͂قƂ�ǂ��ĂȂ��B
���Ȃ̂́A���������u���b�N���̐����S�̂�{���ɂƂ�̂��Ƃ������ƁB
T(x,t) := [K(x+t)^(5/4)] + [K(x-t)^(5/4)] �Ƃ���ƁA
>>764 �̒�`�ɂ�� S(x,t) �Ƃ̊W�� KS-2<T��KS �ƂȂ邪�A
���ۂ� KS(t)-T(t) �� t ���Ƃ� [0,2) �̂ǂ��ɗ����邩�𐧌䂷��̂͂قڕs�\�B
������ t �� 0 ���炠��l�܂ő��₵�Ă��������� T(x,t) �̒l���A�Ⴆ��
100, 101, 102, 104, 105, �c
�̂悤�ɂ���l�����\����r���ł��Ȃ��B
����� K ���\����������߂ĉ����ł�����ł��Ȃ����A
���ɗǂ����@��������Ȃ�����́A�����炭�ȒP�ɂ͖������Ȃ�
�Ƃ͌�������ł��A�萔 K>0, c>1 ��K�ɂƂ��
�A�������̐��̐����̂������Ȃ��Ƃ������ [Kn^c]+[Km^c] �ƕ\����A�Ƃ���
�܂��܂��Ȍ��ʂ͓����邯�ǂ���
�l�I�ɖʔ����Ǝv�������N�̂Ƃ��钆�w�̖�肾���ǂ������ȁH
167�H
>>769 �����Ȃ�قǁA�������̓_�����
�C���C���A�҂đ҂�
>>771 �@�u167�v���Ⴀ��܂���@�ʔ����������͂���܂���
�@�܂�2022=6�~337����A337�~a=������674(a��6�̔{��)�ƍl���܂�
>>770 �Ђ����琔�����
> calc(2022,6,674)
[1] 167
���p���
1234�ɂ��鐮����������ƁA7�����̐���������888�ƂȂ�
���鐔�����B
> calc(1234,7,888)
[1] 132 632 1132 1632 2132 2632 3132 3632 4132 4632 5132 5632 6132 6632 7132 7632
�����A�������g���鐔�h��167���
>>773 �H
t��1���������� [(x+t)^c] + [(x-t)^c] �̍���2��1(��0)������
[(x+t)^c] ���̂��̂͂����Ƒ傫�������͂�
t ��(x�Ɉˑ�����)������x�傫���������
>>779 �����
�������セ��Ȃ��ƂȂ���Ƃ킩�������ǖZ�����Ē����ł��Ȃ�����
�܂�[ ]���o������Ƃ�����ƃp�b�Ə�������肪�v�������
>>690 ��BC�ɐ����Ȓ�����l�Ƃ���
BF �� BF��l�ւ̎ˉe�̒���
. = AF sinF + AB sinB
. = CD sinC + DE sin E
�ɂ��
2BF �� AF sinF + AB sinB + CD sinC + DE sin E
. = AF sinC + AB sinE + CD sinC + DE sin E
���l�ɂ���
2DB �� CBsinE + CD sinA + EF sinE + FA sin C
2FD �� EDsinA + EF sinC + AB sinA + BC sin C
����Đ����藝���
4(Ra+Rc+Re)
= 2(BF/sinA + DB/sinC + FD/sinE)
�� (AF sinC + AB sinE + CD sinC + DE sin E)/sinA
+(CB sinE + CD sinA + EF sinE + FA sin C)/sinC
+(ED sinA + EF sinC + AB sinA + BC sin C)/sinE
= AB(sinE/sinA+sinA/sinE)
+ BC(sinE/sinC+sinC/sinE)
+ CD(sinC/sinA + sinA/sinC)
+ DE(sinE/sinA + sinA/sinE)
+ EF(sinE/sinC + sinC/sinE)
+ FA(sinC/sinA + sinA/sinC)
�� 2(AB+BC+CD+DE+EF+FA)
>>774 2022�~167����337674����Ȃ��H
>>776 �@
>>783 �@�����ł�
167�͂��������ł����ˁB
>>774 �ł̃t�H���[������Ȃ��Ă��݂܂���
���ʔ����������Ƃ��
�@�܂�2022=6�~337����A337�~a=������674(a��6�̔{��)�ƍl���܂�
�A��3����674(=337�~2)�Ȃ̂�a�̉�3���́u002�v�ɂȂ�܂�
�Ba�̐�̈ʂ̐������߂܂��B337��������3���ɂȂ鐔��1��2�݂̂ŁA
�@1002��6�̔{���ł����A2002��6�̔{���łȂ��̂�a=1002
������1�~337=337�ł��B
�������Ă������肠�肪�Ƃ��������܂����I�@���Ȃ݂Ɉ��m�����C���w�̖��ł���
�@�@�������@�f�������@���݂��邱�Ƃ������B
>>785 �@�@�@�����Ȃ������炱������Č����������
�Ӗ��킩�������������
�@�@���Ł@�����Ȃ��Ƃ����\�����������琔�w�ł͕��ʁA������Ɖ��肵�Ĕw���@���g���B�@�@���̕��@�����ꍇ�͂����̃L�`�K�C
>>789 �������O���w�E����Ă邩����킩���ĂȂ����H
��̕��Ƃ��݂Ă��炨�O�̏������߂郌�x���ɂ͂Ȃ��̂킩���H
>>790 >>791 �܂����O�ɂ͐��w��������
���߂�
>>792 >>785 �ڂ�p���w�C�ӂ̑f���x���w����f���x�ɂ��Ȃ���
���̂ǂ����̈Ӗ��ɂ��Ƃ�����Ă���
(A) �ǂ�ȑf��p�Ɛ���n���Ƃ��Ă��An^p-p �� q �̔{���ɂȂ�Ȃ�
(B) �K�ɑf��p���Ƃ�A�ǂ�Ȑ���n���Ƃ��Ă� n^p-p �� q �̔{���ɂȂ�Ȃ�
�w���@�̗��ĕ�����(A)���ȂƐ����͂ł��邯�ǁA
���߂̕���������悤�ȏ������͔�����悤�ɂ��Ă�
��Ŋ̐S�̖��̕������ǁA�������������
��̓I�ɉ����̑f���Ő��藧���Ƃ��m�F���Ă���o�肵�Ă��ł͂Ȃ��H
(p,n) = (q,0) �Ƃ����� n^p-p = -q ������ q �Ŋ��肫��邩��咣�͐��藧���Ȃ�����
����(A)����Ȃ���(B)�̉��߂Ȃ�A
(p,q)=(2,5) �Ƃ���Ίm���� n^2-2 ��5�ł͊���Ȃ�����A���Ƃ��Ă͐��藧��
>>794 �@�@���O�ɂ͐��w�I�Ȓm�����������Ȃ��@�@���l�������Ă��܂��܂��������̂��Ƃ���
���O�ɁX��{�I�Ȑ��w�I�p��̎g��������ł��ĂȂ�
�@�@�@�@�@���w�̒����͕��ՓI�Ȑ^�����������`�łȂ����Ă��鍂�����̑��݂Ȃ̂ŃN�Y�ɂ͕�����Ȃ�
�������ʔ����Ǝv���Ă����ꂪ��ʓI�ɐ��藧�Ƃ͌���Ȃ����A����͐��藧���Ȃ��ǂ��납���͂����[���ᔽ���Ăė������炵�Ă��炦�Ȃ��Ⴞ�ȁB
�@�@n^p-p=kq�@�@�@�܂�@�@n^p = kq+p�@�@���w���ł��邱�Ƃ��ؖ����邽�߂̍l�������i�Ƃ��Ď��̂��̂�����
�@�@�@�t�F���}�[�̏��藝���g�������Ƃ��낾�����̒藝�́A�@�@n,p���݂��ɑf�Ƃ�������������A�g����̂��g���Ȃ��̂��悭������Ȃ��藝�ł���
�@�@�Ⴆ�A�@�@2^(p-1) �߁@�P�@( mod p)�@�@�̂悤�ȏꍇ�́A�t�F���}�[���藝�ɂЂ����Ă���݂��ɑf�̏������ł��邽�߁A���p�ł��邪�A
�@�@���́A�@�@n^p�@�߁@p �imod q)�@�@�Ƃ������Ƃ������Ă���͖̂��炩�ł���B
�@�@2^p �߁@p (mod q)�@�̏ꍇ�ŁA�@�@�t�F���}�[�̏��藝����@�@2^(p-1)�@�߁@1 (mod p)
�@�@�@�����Ŗ��ɂȂ��Ă���̂́A�@�@n^p = kq+p�@���w���ł��邱�Ƃ������藝���F���l�������Ă���
�K�_�K�^�����ăX���r�炷�Ȕ\����
�@�@�o�J�͂��O���@�@���Ⴀ�ˑR�A��s�@�����ƌ����Ă��O�͔�s�@������̂��H
�������������ɓ��e����ׂ��������Ɠǂ�
�@�@������@�@n^p = kq+p�@�@���w���ł��邱�Ƃ�����������
�@�@���ꂪ�w���ł��邱�Ƃ��������@�͂��邪���ɓ���A�����
Since (pp !1)=(p!1) = 1+p+p2 +�� �� ��+pp!1 �L p+1 (mod p2), we can get at
���X���̌��ׂ��炵�đf�����͖����ɑ��݂��邱�Ƃ���AQ�̏��k�̃K���A��Ƀ`�F�{�^���t�̖��x�藝��K�p���Ă��̂悤��q�̏W���́A1/p�̖��x�������Ƃ��킩��A�����ɑ�����q�����Ă���Ƃ����邪�A�f�����������ɑ��݂��Ă��邱�Ƃɒ��ڂ��Ă��A���̂悤�ɓ���藝�ɂ�邵���Ȃ���A���̉�@�͐��w�E�̒��ł����ɍ����\�ȉ�@�ł���Ȃ��Ȃ��v�����Ȃ����Ƃ��g�ݍ��킹�Ă��背�x���������B���Z���x�̐��w�̖��̒��ł��ō���Ɉʒu����ƌ����Ă悢�B
���������̖�肷��܂��N�ɂ��`����ĂȂ���o�[�J
�@n^p = kq+p���w���ł��邱�Ƃ��������Ƃ��Ă����Ⴒ���ᖵ���������Ƃ����� >>812 �n�C���x��wwwww
�S�̓h�������܂������ł����ł��B
�P�ʂ̓��[�g���ő����ė��܂������A�v�Z�����109���ĂɂȂ�܂����B����Ȃɂ����ł����H���ĒP��2000�~����3�����炢�̍H�����ȂƐ���ɓ`���܂������A���̌v�Z����218,000�~�̍H���ɂȂ��Ă��܂��܂��B�{��ꂻ���ł��B
��낵�����肢���܂��B�S�Ă̏c�𑫂��������ɉ��̐����𑫂����̂������܂����B
�U�����悤�Ǝv�����炢�̊Ԃɂ킩�X�������Ă��c
>>817 �����͎���X������Ȃ��̂Łi
>>1 �͓ǂ����ˁj
�ȒP�ȓ��e�ۂ�����Ƃ肠�����������ŋ����Ă�����Ƃ��Ł�
���Z���w�̎���X�� Part417
http://2chb.net/r/math/1648557700/ >>818 ���肪�Ƃ��������܂��I������ɏ������݂��Ă݂܂��B���݂܂���ł����B
Hn��n�Ԗڂ̒��a���A��(x)���[�[�^���Ƃ���
>>820 ���a���ăR����
https://ja.m.wikipedia.org/wiki/%E8%AA%BF%E5%92%8C%E6%95%B0#: ~:text=n%20%E3%81%BE%E3%81%A7%E3%81%AE%E8%87%AA%E7%84%B6%E6%95%B0%E3%81%AE,%E8%80%85%E3%81%AE%E5%90%8D%E5%89%8D%E3%81%A7%E3%81%82%E3%82%8B%E3%80%82
����Ƃ��t���a���ȂH
wiki�̕��͖������邩���������炵������t���a�̕��H
�����ł��A�t���a�̕��ł�
H(n)�̕����g(x) = -log(1-x)/(1-x)�͙p�W�J����Γ�����
Hn = ��[k=1,n]1/k = ��[k=1,��]n/(k(n+k))
�@�@�i�P�j�@�@����ȒN���ǂ�ł��Ȃ��Q�����˂�̔�
2�����ɂ�����f�ȕ��X���āA���w�����ȏ�Љ��ς��Ȃ��Ă͂Ȃ�Ȃ����Ďv�z�������Ă邱�Ƃ������ł���
���̃X���Ŗ��o���Ă����l�݂͂�Ȏ��������̓������猩����������Ƃ����������Ȃ�����H�v���Ė��`���ɂ��ĉ��p�ӂ��Ă݂�ȂŊy��������Ă���
��[n=1,��]Hn/n^2
>>820 �ł����A������
>>831 �ƑS���������@�ɂȂ�܂���
>>826-827 ���Q�l�ɂȂ�܂�
(1) ��[n��1�`��] (�|1)^n H_n / n �͐�Ύ����͂��Ȃ��������͂��邱�Ƃ������B
�ϕ��͈͕ς�邾���Ȃ̂ł́H
integral_(-1)^0 log(1 - x)/((1 - x) x) dx = 1/12 (6 log^2(2) - ��^2)≈-0.582241
https://www.wolframalpha.com/input?i=%E2%88%ABlog%281-x%29%2F%281-x%29%2Fx+dx+from+-1+to+0& ;lang=ja
>>835 (1)
Hn/n = ��[k=1,��]1/(k(n+k))
��n�Ɋւ��ĒP��������
1/n��Hn/n��(1+log(n))/n��0 (n����)
�̕]������Hn/n�̘a�͎������Ȃ�����㋉���͎�������
(2)
��[n=1,��](-1)^n Hn/n
= ��[n=1,��]��[k=1,n](-1)^n/(kn)
= ��[k=1,��]��[n=k,��](-1)^n/(kn)
= ��[k=1,��](-1)^k/k^2 + ��[k=1,��]��[n=k+1,��](-1)^n/(kn)
= -(1-2/2^2)��(2) + ��[k=1,��]��[n=1,��](-1)^(n+k)/(k(n+k))
���̓ڂ̘a��
d/dx ��[k=1,��]��[n=1,��]x^(n+k)/(k(n+k))
= -log(1-x)/(1-x)
= d/dx (1/2)log^2(1-x)
�ȏ�܂Ƃ߂��
��[n=1,��](-1)^n Hn/n = -(1/12)��^2 + (1/2)log^2(2)
>>837 (2)�͈ȉ��̉ɍ����ւ�(��Ύ������Ȃ��̂Řa�̌����͒��ӂ��K�v�ł���)
��[n=1,��]x^n Hn/n
= ��[n=1,��]��[k=1,n]x^n/(kn)
= ��[k=1,��]��[n=k,��]x^n/(kn)
= ��[k=1,��]x^k/k^2 + ��[k=1,��]��[n=k+1,��]x^n/(kn)
= ��[k=1,��]x^k/k^2 + ��[k=1,��]��[n=1,��]x^(n+k)/(k(n+k))
= ��[k=1,��]x^k/k^2 + (1/2)��[k=1,��]��[n=1,��](x^(n+k)/(k(n+k)) + x^(n+k)/(n(n+k)))
= ��[k=1,��]x^k/k^2 + (1/2)��[k=1,��]��[n=1,��]x^(n+k)/(nk)
= ��[k=1,��]x^k/k^2 + (1/2)log^2(1-x)
�����x=-1�������A�[�x���̒藝���ȉ������藧��
��[n=1,��](-1)^n Hn/n = -(1/12)��^2 + (1/2)log^2(2)
�܂���������Hn�̕����-log(1-x)/(1-x)�Ɗ��ƃN�Z�̂Ȃ��������ɂȂ��Ă邩�炻���܂œ���Ȃ�
Geogebra�ŗV��ł��Ă��܂��܌��������̂ł���
���ꂠ���Ă�H
���f���ōl���ꎟ�ϊ� z -> 1/z ���s���ƁA
�������Ԋu�ɂȂ���
>>678 1990�NIMO�������̑�3��
��� (cf. Sierpinski gasket ) p��f���Av��p�i�t�l�Ƃ���Ƃ�
v(C(n,k))��v(n)-v(k)
(������v(0)=���Ƃ���)
(��) C[n,k]�Ɋւ���induction
C[n,k]=1�Ȃ�k=0,n������RHS��0�Ő���
C[n,k]<M�ł悢�Ƃ���C[n,k]=M�Ƃ���
p | n�łȂ����RHS��0��薾�炩
p | n�Ƃ���
�K�v�Ȃ�k��n-k�Ɏ��ւ���k��n/2�Ƃ��Ă悢(�� RHS>0�Ƃ��Ă悢����v(n)>v(k)�ł���v(k) = v(n-k) )
l��k�ȉ��̍ő��p�̔{���Ƃ���Ηe�Ղ�
v(C[n,k]) �� v(C[n,l]) �AC[n,k]��C[n,l]�Av(k)��v(l)
�ł���
���̂Ƃ�
v(C[n,k])
�� v(C[n,l])
= v(C[n/p, l/p]) (cf. Sierpinski gasket )
�� v(n) - v(l) ( �� Assump. of the ind. )
�� v(n) - v(k). ��
���@
>>845 �R�s�y�~�X
��� (cf. Sierpinski gasket ) p��f���Av��p�i�t�l�Ƃ���Ƃ�
v(C(n,k))��v(n)-v(k)
(������v(0)=���Ƃ���)
(��) C[n,k]�Ɋւ���induction
C[n,k]=1�Ȃ�k=0,n������RHS��0�Ő���
C[n,k]<M�ł悢�Ƃ���C[n,k]=M�Ƃ���
p | n�łȂ����RHS��0��薾�炩
p | n�Ƃ���
�K�v�Ȃ�k��n-k�Ɏ��ւ���k��n/2�Ƃ��Ă悢(�� RHS>0�Ƃ��Ă悢����v(n)>v(k)�ł���v(k) = v(n-k) )
l��k�ȉ��̍ő��p�̔{���Ƃ���Ηe�Ղ�
v(C[n,k]) �� v(C[n,l]) �AC[n,k]��C[n,l]�Av(k)��v(l)
�ł���
���̂Ƃ�
v(C[n,k])
�� v(C[n,l])
= v(C[n/p, l/p]) (cf. Sierpinski gasket )
�� v(n) - v(l) ( �� Assump. of the ind. )
�� v(n) - v(k). ��
�ׂ���a�k^p��p��3�ȏ�̊�̎��k^p=q�����f��q�͑��݂��邩
�@�@���ȒP�ŏ����I�Ȗ��ɑ��鍂�x�ȉ�^�����Ȃ����_�Ł@�@�E�\�ŃN�\�F��
����ς葶�݂��܂����
>>852 p|S(p)�Ƃ͉���\���Ă��܂����H
>>848 ��k^p = 1^p + 2^p +...+ n^p �Ƃ���
n=2�̂Ƃ�
��k^p �� 1-1 �� 0 (mod 3), ��k^p>3
n��4�̔{���̂Ƃ�
��k^p �� 1+0-1+0+...+1+0-1+0 �� 0 (mod 4), ��k^p>4
n��3�̔{���̂Ƃ�
��k^p �� 1-1+0+...+1-1+0 �� 0 (mod 3), ��k^p>3
n��5�̔{���̂Ƃ�
��k^p �� 1+2^p-2^p-1+0+...+1+2^p-2^p-1+0 �� 0 (mod 5), ��k^p>5
�ȉ����l��
n��r�̔{��(r�͊)�̂Ƃ�
��k^p �� 0 (mod r), ��k^p>r
���������ă�k^p�͑f���ɂ͂Ȃ�Ȃ�
�}�̂悤�Ɍ��~�̔����ɔ��~�����ڂ��Ă���B���~�̔�����S�̂Ƒ������ꍇ�A�S�̂̂������~�̐�߂�䗦��Z�Ƃ���BZ�̍ŏ��l�͂������B
>>842 �@
>>844 P�̍��W�v�Z���ĉ~�̒��S����̃x�N�g����̓��ς��v�Z������cos�̒l��-1/2�ɂȂ������炠���Ă�͂�
�����v�Z�Ȃ�Ő��������\�t�g�g���������悳���Belegant�ȏؖ����~����
>>857 H=2ab/(a+b)
a'=ab/(2a-b) ((2a-b)>0�Ƃ���)
Solve({x^2+y^2-(a+a')*x+a*a =0,x^2+y^2-H*x=0}, {x, y})
P�̍��W {x = ((-a*a')/(H - a - a')), y = ��((-H^2*a*a' + H*a^2*a' + H*a*a'^2 - a^2*a'^2)/(H - a - a'))}
((-a*a')/(H-a-a')-(H/2))*((-a*a'/(H-a-a'))-((a+a')/2))+(((-sqrt(-H^(2) a a'+H a^(2) a'+H a a'^(2)-a^(2) a'^(2)))/(H-a-a')))^2)
= (1/4) (H a + H a' - 2a a') = ���� = (H/2)*((a'-a)/2)*cos��
����� cos��={(2*a*b/(a+b))( a + (a*b/(2a-b))) - 2a^2*b/(2*a-b)}/{( (2*a*b/(a+b)) (-a + (a*b/(2a-b))))}=-1/2
>>858 > Solve({x^2+y^2-(a+a')*x+a*a =0,x^2+y^2-H*x=0}, {x, y})
a*a' ��'��������
�Ō�̕ϐ��u���v�Z�͕֗��ȃR�}���h��������
Expand(Substitute((H*(a+a')-2*a*a')/(H*((a'-a))),{H=2a*b/(a+b),a'=a*b/(2a-b)}))
=-1/2
�O
>>725 >>856 �����ʼn����ƁA
��=3��/(10��-6)
=0.37082173445�c�c
4���ォ�Ȃ����Ċ����B
cos75��=(��6-��2)/4�Ƃ�����g�����B
>>857 >>843 �͓ǂH
a'=1/a, b'=1/b�Ƃ����ƁA
C_0�͓_(a'+b')/2��ʂ�����ɐ����Ȓ����A
C_1�͓_a'��ʂ钆�Sb'�̉~�A
C_2�͓_b'��ʂ钆�Sa'�̉~
�ɂ���B���Ƃ͐}��`���A�p�x���ۑ�����邱�Ƃ��疾�炩
���]������݂��̒��S��ʂ锼�a�̓�������̉~�Ƃ��̂Q��_�����Ԓ����ɂȂ邩��
>>856 ���~�̔�����x=��(1-y^2), cos(t)��y��1�Ƃ����
��/6��t<�� �̂Ƃ����~�̔��a��r = (2 - ��3 cos(t))/4
0<t<��/6 �̂Ƃ����Ȃ�
��
Z = (��/8)(2 - ��3 cos(t))^2/(2t - sin(2t)), ��/6��t<��
���̍ŏ��lZmin��
2 sin(t) - ��3 t = 0 �̐��̉���a�Ƃ���Ƃ�Zmin = ��(2 - ��3 cos(a))/(8a)
a = 0.915582309673212459699344087310133383...
Zmin = 0.405149796624800679921346843672297349...
�O
>>860 >>856 ��Z=(���~��r^2/2)/[���~��/2��-�oh��(1-h^2)�p/2]
=��r^2/�o��-h��(1-h^2)�p
=��r^2/(��-cos��sin��)
Z'�̕��q=2��r(��-cos��sin��)-��r^2(1+sin^2��-cos^2��)=0
(��-cos��sin��)-rsin^2��=0
�O
>>864 >>856 r�ƃƂ̊W�����킩��Ε�����A
����=0�̎���ʼn�����͂��B
�O
>>865 >>856 r=(19-cos�Ɓ�105)/16
r^2=(361-38cos�Ɓ�105+105cos^2��)/256
Z=��r^2/(��-sin��cos��)
=��(361-38cos�Ɓ�105+105cos^2��0)/256(��-sin��cos��)
Z'�̕��q=2��r(��-sin��cos��)-��r^2(1-cos^2��+sin^2��)
=2��r(��-sin��cos��)-2��r^2sin^2��=0
��-sin��cos��-rsin^2��=0
��-sin��cos��-19sin^2��/16+(sin^2��cos�Ɓ�105)/16=0
16��-16sin��cos��-19sin^2��+sin^2��cos�Ɓ�105=0
(�����͂����܂�)
�O
>>867 >>856 ���~�ƌ��~�̔��a�̔��1:4�Ƃ���ƁA
Z=3��/(16��-12��3)=0.31969128035�c�c
1/4��菭���������B
(��-cos��sin��)-rsin^2��=0
2sin��-2��cos��=sin^3��
�O
>>870 �����B
8��cos��-sin3��-5sin��=0
�O
>>871 >>856 ��Z�̎��𗧂āA
r���Ƃŕ\��r�������A
����Z'�̕��q=0���A
8��cos��-sin3��-5sin��=0
��=57.0648791992273���̂Ƃ��A
��=0.99597002927
���~�̔��ar�̎��Ɣ�Z�̎��̃�����T�����B
���Ƃ͑�����邾���B
�����T���B
�O
>>871 >>856 ��Z�̎��𗧂āA
r���Ƃŕ\��r�������A
����Z'�̕��q=0���A
8��cos��-sin3��-5sin��=0
��=57.0648791992273���̂Ƃ��A
��=0.99597002927
���~�̔��ar�̎��Ɣ�Z�̎��̃�����T�����B
���Ƃ͑�����邾���B
�����T���B
�O
>>873 >>856 ���~�̔��a��1�A���~�̔����̌ʂɑ��钆�S�p���ƂƂ���ƁA
���~�̔��a������������������cos��
�����̔�����sin��/2
���~�̔��a��r�Ƃ���ƁA
Z=(��r^2/2)/(��/2-sin��cos��/2)
=��r^2/(��-sin��cos��)
r���Ƃ̎��ŕ\���B
��}���āAy���ɉ����Č��_�Ɍ������`�̒��p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
(1-r)^2=[cos��+��or^2-(sin��/4)^2�p]^2+(sin��/4)^2
1-2r=cos^2��+2cos�Ɓ�or^2-(sin��/4)^2�p-(sin��/4)^2+2(sin��/4)^2
sin^2��-2r=2cos�Ɓ�or^2-(sin��/4)^2�p
sin^4��-4rsin^2��+4r^2=4cos^2�Ɓor^2-(sin��/4)^2�p
sin^4��-4rsin^2��+4r^2-4cos^2��r^2+sin^2��cos^2��/4=0
sin^2��-4r+4r^2+cos^2��/4=0
16r^2-16r+3sin^2��+1=0
r=[8-��o64-16(3sin^2��+1)�p]/16
=[8-4��o4-(3sin^2��+1)�p]/16
=(8-4cos�Ɓ�3)/16
=(2-cos�Ɓ�3)/4
r�̒l�������A
Z=��r^2/(��-sin��cos��)
=��(4-4cos�Ɓ�3+3cos^2��)/16(��-sin��cos��)
Z'�̕��q=(4��sin�Ɓ�3-6��sin��cos��)�E16(��-sin��cos��)-��(4-4cos�Ɓ�3+3cos^2��)�E16(1+sin^2��-cos^2��)=0
32��sin�ƂŕӁX����ƁA
(2��3-3cos��)(��-cos��sin��)-(4-4cos�Ɓ�3+3cos^2��)sin��=0
2�Ɓ�3-2sin��cos�Ɓ�3-3��cos��-4sin��+4sin��cos�Ɓ�3=0
2�Ɓ�3+2sin��cos�Ɓ�3-3��cos��-4sin��=0
2(��+sin��cos��)��3=3��cos��+4sin��
12��^2+24��sin��cos��+12sin^2��cos^2��=9��^2cos^2��+24�� sin��cos��+16sin^2��
12��^2+12sin^2��(1-sin^2��)=9��^2(1-sin^2��)+16sin^2��
3��^2+9��^2sin^2��=4sin^2��+12sin^4��
3��^2(1+3sin^2��)=4sin^2��(1+3sin^2��)
1+3sin^2�Ɓ�0
3��^2=4sin^2��
�Ɓ�3=2sin��
2sin��-�Ɓ�3=0
��=0.91558230967322�c�c
(��=52.4590021411��)
�Ƃ̒l�������A
r=�o2-cos(0.91558230967322)��3�p/4
=0.23615282276�c�c
�Ƃ̒l�������A
��Z=��(4-4cos�Ɓ�3+3cos^2��)/16(��-sin��cos��)
=��[4-4cos(0.91558230967322)��3+3�ocos(0.91558230967322)�p^2]/[16�o(0.91558230967322)-sin(0.91558230967322)cos(0.91558230967322)�p]
=0.40514979662�c�c
��ABC�̓����ɓ_P������
>>875 �q���g���Ȃ������܂�
�Ђ�����S�v�Z�H
(1)�͊ȒP�����
�݊p�O�p�`�̂Ƃ��͐��S���O�p�`�����ɂ����ď����������Ƃ͊m�F�ł���B
���S�̂Ƃ���������H
��s(B2)=s(B-B1)=3/��5,
���A����A
�v�Z�Ԉ���ĂȂ���Β��p�ӎO�p�`�̂Ƃ��ɂ������Ȃ�6���Ȑ��ɂȂ�������
�o��҂炵���l�̃��X���S�R�Ȃ�����o��~�X���������p�^�[������
q���A|q|<1�������f���Ƃ���
�m�[�q���g�͓������̂Ńq���g�o���Ƃ��܂�
>>884 ����
> k,l��{0,1}�ɑ��Ďw�W�t���Ɗ�(Auxiliary functions)��kl(z,t)��
> ��kl(z,t)
> = ��[n-k/2��Z] q^(n^2) exp(��inl+2��inz)
> �Œ�߂�
�ł���
q�̌��̂Ƃ��낪��������Ă܂�
a,b,c>0 a+b+c��3/2
>>887 ��((px+q)^2 + 1/x^2) �͓ʊ��ł���
���ۓK���ɃX�P�[���ϊ�����p=1�Ƃ��Ă悭���̏ꍇ2�K������
((3 q^2 x^2 + 8 q x^3 + 6 x^4 + 2) abs(x))/(x^4 (x^2 (q + x)^2 + 1)^(3/2))
�ƂȂ萳�l���Ƃ�
�����f(a,b,c)�͓ʊ��ł���[�_�Ɍ�����������������̈���ŗB��̍ŏ��l���Ƃ�_������
�Ώ̐�����a=b=c�Ƃ��ėǂ�
���̎�
f(a,b,c) = 3 �� (a^2+(1/a^2))
�ł��邩�炱�̍ŏ��l�����߂�ŏ��l�Ă킠��3��2�ł���
>>888 ��蕶�ɂ͐������a+b+c��3/2������̂ōŏ��l��(3/2)��17���Ǝv��
>��((px+q)^2 + 1/x^2) �͓ʊ��ł���
>...
>�����f(a,b,c)�͓ʊ��ł���
�̘_�����悭�킩��Ȃ��̂łł���ΐ������肢���܂�
�܂��������敽��2��łقډ����Ă��܂���肾����...
>>889 f(x,y,z)���ʊ��́�pqrsuv f(px+q,rx+s,ux+v)���ʊ�
�܂�C�ӂ̒�����œʊ��ɂȂ��Ă���Ηǂ�
�{��̊��́�~�~�R�̘a�Ȃ̂Ŋe�X���ʊ��Ȃ�ʊ�
��~�~�́~�~�����̕ϐ��Ɉꎟ�������ƑS����((�ꎟ��)^2+1/(�ꎟ��)^2)�̃^�C�v�ɂȂ�̂ŃR�������ł��ʊ���������Ηǂ�
�K�v�Ȃ畽�s�ړ�����1/(�ꎟ��)^2��1/t^2�Ǝv���Ă������萔����o���ā�((t+a)^2+1/t^2)�̃^�C�v�Ɍ��肵�ėǂ�
����搶��2�����>0����
>>891 ���肪�Ƃ��A�����ł����B
��Ώ̂̉����o���肾�Ƃ����Ɩʔ����Ǝv���B
���łɑ������敽�ς��g����\���Ă����܂��B
f/3 �� ((a^2+1/b^2)(b^2+1/c^2)(c^2+1/a^2))^(1/6)
�� (a^2+b^2+c^2 + 1/a^2+1/b^2+1/c^2 + (abc)^2 + 1/(abc)^2)^(1/6)
�� (3(abc)^(2/3) + 3/(abc)^(2/3) + (abc)^2 + 1/(abc)^2)^(1/6)
�ŏ��̕s�����œ������� �� a^2+1/b^2 = b^2+1/c^2 = c^2+1/a^2 �� a=b=c
2�ڂ̕s�����̓�����������������Ɠ���
g(x) �� 3x^2 + 3/x^2 + x^6 + 1/x^6 �ƒu��
g'(x) �� -6(1-x^4)(1+x^4)^2/x^7 �� 0 (0<x��1/2)
�䂦��
f �� 3(g((abc)^(1/3)))^(1/6)
�� 3(g((a+b+c)/3))^(1/6)
�� 3(g(1/2))^(1/6)
�� (3/2)��17
�Ō�̕s������a+b+c=3/2�̂Ƃ��ɓ��������藧��
>>884 �̖��
>����00(x[j]) - ����01(x[j]) - ����10(x[j]) + ����11(x[j])
>=2����00(y[j])
������wolfram�搶�Ɛ��l������Ȃ�
���������Ęa�łȂ��Đ�
����00(x[j]) + ����01(x[j]) - ����10(x[j]) + ����11(x[j])
=2����00(y[j])
�̌��H
>>893 ���炵�܂���
�ςł�
����00(x[j]) + ����01(x[j]) - ����10(x[j]) + ����11(x[j])
=2����00(y[j])
������
���̓ǂ��ȏ��ł̓ƊԌ`���Ƃ������O���t���Ă܂���
���A�܂��Ԉ���Ă�
>>895 �܂�����orz
����00(x[j]) + ����01(x[j]) + ����10(x[j]) + ����11(x[j]) = 2����00(y[j])
�S���v���X�ł�
���
�㐔���̒l��̏���A�����͌W���̂̑㐔�I�g��̌�
���ʏ�ɉ~�Ƃ��̒��S���^�����Ă��鎞�A��K�݂̂�p����
(1)�`(3)�͏���ԍ��ł�
���̐ݒ�ŕ��ʂɕ��f���W���^�����Ă���Ƃ���}����Ă���~��|z|=1�ł���0,1�͍�}����Ă����_�Ƃ���
���@a,b��S��R��a+b��S
�g�����v���䂪�܂������ɂł���t���^�̋Ȑ��̈�ʎ������߂�
>>667 Wiki�̕���1�B
�F���ۃ^�C�q�~�����[���_�i�����イ�����^�C�q�~�����[����A�p��: Inter-Universal Teichmüller Theory�A����: IUT�j�́A���w�Җ]���V��ɂ���ĊJ�����ꂽ�A���_�ɂ����邳�܂��܂ȗ\�z�A����ABC�\�z�������v��[1]�̍l�@�ɂ��A���A�[�x���Ȃǂ��g�債�����̉F���� (IU) ���\�z�������w���_�ł���[2]�B
���l�@�œ����uABC�\�z�������v���v�Ə�����Ă���B
2008�N�̕���1������V�_���̌�t���͂łȂ���A���z�̃t���[�}�́A
�X�^�[�g�́uABC�\�z�����������v����n�܂邪�A
���g���Łu�d�v�ȃ|�C���g�v�ƂȂ��Ă���A�u�ʏ�̏W���_���g�傷��K�v������v�Ƃ��āAABC������������œ������������Ŋ̂ł��邱�Ƃ�������B
�m�X���u����܂łɂȂ����w�ւ̐i���v���܂܂ꂽ�Ƃ���Ř_�c���N���Ă���A���̐V�������w�̉�������߂���ɑ��AAND��OR�̘_�����ł���Ƃ����B
�����番����Ղ��Ȃ�悤�ɃA�u�X�g���N�g��t�����̂ł͂Ȃ��̂��ȁB
�ǂ�����@�̏��ŁA�ǂ������@�̏�����������āA
�V���Ș_���W�J��AND�ŒS�ۂ��Ă���Ƃ̐����iOR���g���̂͌��j�Ƃ̘_�|�ɂȂ����B
���A�X���Ⴂ�̋L�������܂����B���Ɏ��炵�܂����B
>a��ʂ�2�ڐ�����}�\�Ȃ̂͊��o�Ȃ̂�2�ړ_��u,v�Ƃ���
�C���A�L���Ⴂ�o�Ȃ�����
>>901 ��ai��a��i�����Ԓ�����im(z)=1/2�̌�_��=(a+i)/2���܂���}������a�����Ԓ��O�Ƌ����̌�_��ai�ł���
����a��i�����Ԓ�����̓_��a������łȂ��H
>>908 ����A����
���@a��S��R �� ai,�}a�}i, �}ai �}1��S
(��) ai��a+i�ɂ��Ă��������Ώ\���ł���
ai��a��i�����Ԓ�����im(z)=re(z)�̌�_�����܂���}������1�����Ԓ��O�Ƌ����̌�_��ai�ł��邱�Ƃ���킩��
����a+i��a��i�����Ԓ�����im(z)=1/2�̌�_������}������0�����Ԓ�����im(z)=1�Ƃ̌�_��a+i�ł��邩���}�\�ł��遠
�O
>>874 >>903 (x^2+y^2-1)^3=x^2y^3
�܂���y=x^4
�܂�Ȃ����������
�f�J���g�̉~�藝���
�O
>>910 >>911 ���~C�̔��a��r�Ƃ���ƁA
�s�^�S���X�̒藝���A
��o(5+r)^2+(5-r)^2�p+��o(2+r)^2+(2-r)^2�p=��o(5+2)^2+(5-2)^2�p
��(20r)+��(8r)=��40
��(5r)+��(2r)=��10
5r+2r��10+2r=10
(7+2��10)r=10
9r=10(7-2��10)
��r=(70-20��10)/9
=0.75049408851�c�c
�~����ɑ��قȂ�4�_ABCD�����̏��ɕ���ł���
>>912 �@���a�����ɂ���̖Y��Ă�...�X�}��
https://imgur.com/a/r9gzuXC ㋐〜㋤�ɓ��Ă͂܂�0〜9�̐����܂���-������B
>>912 A�̔��a��a�AC�̔��a��c�Ƃ���ƁA���S�Ԃ̋�����a+c�A���S�̏c�̍���a-c������
���S�̉��̍��̕����́@(a+c)^2-(a-c)^2=2a*2c
���l��B��C�̒��S�̉��̍��̕�����2b*2c�AA��B�̒��S�̉��̍��̕�����2a*2b
��̓�̉��̍��̘a2��c(��a+��b)����̉��̍�2��ab�ƈ�v���@c=ab/(��a+��b)^2
���SO���ar�̉~C�ɑ��ĕ��ʏ�̓_A��O�ɑ��ĕ�����l:{P|OA���EOP��=r^2}�ɂ���Ē�߂��钼��l��Ή�������
r^2=OP(��)�EOQ(��) (�x�N�g��OP��OQ�̓���)�̕����V���v�����.
>>921 >>920 ��915�̑z����̈ꕔ���ł�
���Ȃ킿915�̐ݒ��
OP²+OQ²=PQ²+2r²
�������̂�915�̑z����ł�
>>921 �����Y��܂������ǂ��ꐳ���ł�
�����Đړ_S,T��P(u,v)�̋ɐ��̕�����ux+vy=r²�������Ƃ���(��ڐ��̕������̌���)����ST��P�̋ɐ����Ɖ���܂�
�܂�915��915�̐ݒ�̌���
�uQ��P�̋ɐ���ɂ��鎖�������v
�Ɠ����Ƃ킩��܂�
C[7,k]��k=0����7�܂ŕω����������̒l�����ɏ����ƁA{1,7,21,35,35,21,7,1}
>>924 aₙ, bₙ,cₙ��0��n<3ᵉ�ɑ���C[n,k]�̒��́�0,��1,��2 (mod 3)�ƂȂ�k�̐���^�����Ƃ���
�����o����
a: 0 0 0 2 1 0 4 2 0�d
b: 1 2 2 2 4 4 2 4 5..
c: 0 0 1 0 0 2 1 2 4..
�ł���A���������͑�0�����琔����Ƃ���
aₙ+bₙ+cₙ=n+1�ł��邩�������bₙ+2cₙ=n+1�Ɠ��l�ł���
�e��̏�������3ᵉ�������o���ē����镔�����aᵉ, bᵉ, cᵉ�Ƃ���
�p�X�J���̎O�p�`����Q����
bᵉₙ₊₁=bᵉₙ⊕2bᵉₙ⊕2bᵉₙ+cᵉₙ
cᵉₙ₊₁=cᵉₙ⊕2cᵉₙ⊕2cᵉₙ+bᵉₙ
��������A������⊕�͂Q�̗L������q���ē�����L�����^������Z�q�Ƃ���
�Q������p���Ĉȉ��̎咣���A�[�I�Ɏ������
�咣�@0��n<3ᵉₙ�An = k�~3ᵉ + l, (k = 1,2, 0��l<3ᵉ⁻¹) �Ƃ���ȉ�����������
bₙ+cₙ = 3ᵉ (n = 3ᵉ - 1)
. �� 2�~3ᵉ⁻¹ (n �� 3ᵉ - 1)
bₙ+2cₙ = (3n+1)/2 ( n = 2�~3ᵉ⁻¹- 1)
. = (3n+2)/2 ( n = 3ᵉ - 1)
. = n+1 ( n = 3ᵉ - 2)
. < n+1 ( n = 2�~3ᵉ⁻¹- 1,3ᵉ - 1,3ᵉ - 2)
�咣�ɂ�苁�߂�n�̏�����n+2��3�̃x�L�ƂȂ鎞�ł���
>>925 ��O�̑I�ѕ����Â�����
bₙ+cₙ�̕��͍����Ă�
bₙ+2cₙ>n+1�ƂȂ��O��n = 2�~3ᵉ⁻¹- 1, 3ᵉ- 4, 3ᵉ- 1�̂R�����
���肪�Ƃ��������܂��B
>>927 ������V�F���s���X�L�[�̃K�X�P�b�g�ł�
�p�X�J���O�p�`��3�Ŋ��������܂��
�P
�P�P
�P�Q�P
�P�O�O�P
�P�P�O�P�P
�P�Q�P�P�Q�P
�P�O�O�Q�O�O�P
�P�P�O�Q�Q�O�P�P
�P�Q�P�Q�P�Q�P�Q�P
�̂悤�ɂ����̃t���N�^���}�`�̍\��������܂�
��̎O�p�`�̒��ɏ������O�p�`��9��
��
����
������
�̌`�ŏo�����ā��̊O���ɂ͂O�������܂���(���̒i���灢�̒��ɂ��O���o�܂������̊O���ɂP�A�Q���R��o�邱�Ƃ͂���܂���)
����ĂP�̐�bₙ�ƂQ�̐�cₙ�͂��́��̒���������悢�Ƃ킩��܂�
�傫���O�p(���̍�)�̂P�i�ڂ͏������O�p���̂��́A���Ȃ킿b₁₊₁�̏o����1/3��bₙ���̂��̂����܂�
���̒i�ɂ́��Q���A���Ȃ킿2bₙ�����܂�
�Ō�̒i�̗��[�ɂ���O�p�`�́����̂��̂ł����^�́��͒��_���Q�ɂȂ�̂Ł��̂P�ƂQ�����ւ������̂ɂȂ肻���Ɍ����P�̐���cₙ�ƂȂ�R�i�ڂ�2bₙ+cₙ�ƂȂ�܂�
��������
bₙ₊₁=bₙ⊕2bₙ⊕2bₙ+cₙ
��bₙ�̖������ׂ��Q�����Ƃ킩��܂�
cₙ�����l�ł�
>> bₙ₊₁=bₙ⊕2bₙ⊕2bₙ+cₙ
����
>>929 ����Ɖ��t���ԈႦ�܂���
bᵉ⁺¹=bᵉ⊕2bᵉ⊕2bᵉ+cᵉ
cᵉ⁺¹=cᵉ⊕2cᵉ⊕2cᵉ+bᵉ
�ł�
�Ⴆ��e=1�̏ꍇ����e=2�̏ꍇ���v�Z����̂�
b¹=(122)�Ac¹=(001)
�Ȃ̂�b²���v�Z����ɂ͂܂�����3�̗�
b¹=(122)
2b¹=(244)
2b¹+c¹=(245)
�Ȃ̂�
b²=(122244245)
�Ƃ킩��܂�
���l�ɂ���
b²=(001002124)
�ƂȂ�܂�
���ۂX�i�ڂ܂Ńp�X�J���O�p�`�����Ă݂��
�P
�P�P
�P�Q�P
�P�O�O�P
�P�P�O�P�P
�P�Q�P�P�Q�P
�P�O�O�Q�O�O�P
�P�P�O�Q�Q�O�P�P
�P�Q�P�Q�P�Q�P�Q�P
�ƂȂ���b,c���������P�̐��A�Q�̐���\���Ă��鎖���킩��܂�
���J�Ȑ����A���肪�Ƃ��������܂��B
�Ȃ�قǁA���̈Ӗ���������܂����B
�V�F���s���X�L�[�̃K�X�P�b�g�@�̍\���̍ċA����
bᵉ⁺¹=bᵉ⊕2bᵉ⊕2bᵉ+cᵉ
�̗l�Ȍ`�Ŏ����ꂽ��ł��ˁB�����܂����B
�قƂ�ǐ������Ǝv���܂��B
>>926 �ł������u��O�v�Ƃ��ď�����Ă�����̂�����܂����A���ɂ�����Ǝv���܂��B
�����u��O�v�̋��ʓ_���l����ƁA�ʂ̃A�v���[�`�������Ă��邩������܂���B
>>933 ����܂���
�v�Z�@�ŒT���Ă݂܂���
�ŏ�����g���悩����
�ꕔ����(3�i�\��4���̂��5���̂��)
(44,"1122",36,"1100",52,"1221")
(50,"1212",36,"1100",52,"1221")
(52,"1221",36,"1100",52,"1221")
(53,"1222",54,"2000",80,"2222")
(71,"2122",54,"2000",80,"2222")
(77,"2212",54,"2000",80,"2222")
(79,"2221",54,"2000",80,"2222")
(80,"2222",81,"10000",121,"11111")
(134,"11222",108,"11000",160,"12221")
(152,"12122",108,"11000",160,"12221")
(158,"12212",108,"11000",160,"12221")
(159,"12221",108,"11000",160,"12221")
(161,"12222",162,"20000",242,"22222")
(215,"21222",162,"20000",242,"22222")
(233,"22122",162,"20000",242,"22222")
(239,"22212",162,"20000",242,"22222")
(241,"22221",162,"20000",242,"22222")
(242,"22222",243,"100000",364,"111111")
����n�A�^��bₙ+cₙ�A�E������bₙ+2cₙ�Łgn��3�i���\���ɂO�͂Ȃ��ō��ʈȊO�̂P�̐������X1�h�̏ꍇ
�����l�ł����B��O�Ƃ��Ă������̂�������ƁA���؉��ɔ[�߂��Ă���̂ŁA���S���Ǝv���܂��B
�y�ߕ�z�A�����J�Łu�N�C�Y�~���I�l�A�v�̍Ō�ɏo���ꂽ��肪�K�`�œ������Ƙb��ɂ�����
http://2chb.net/r/poverty/1651840469/ (1) �I����4�̓��A3�͕s������1������
������C�Ȃ�A25%�ɂȂ��Ė������Ȃ��H
�ʃX���̏Љ�ɂ��ƌ��l�^�̓X�}�������̘_���p�Y���̖{�炵��
�O
>>914 >>937 (c)50%
��25%�Ƃ��������������I�����ɑ��݂��A�����͐����ł͂Ȃ��B
�������ɂǂ��炩����������Ȃ瑼���͕s�����ƂȂ�A�����������������s�����ƂȂ薵�����邩��ł���B
����Đ�����0%��50%��2���ƂȂ�A
�m����1/2���Ȃ킿50%�ł���B
���ϋɓI��(c)��I��ł����B
���l�ʑ̂�a,b,c,d����������ō~�����Ƃ���c���o��m����50%�ł����
����ׂɓ�����c����ʂɂȂ����Ƃ���c���o���ƌĂ�
�C���A���̖��̍�҂́u50%�������v�Ɛݒ肵���̂�������ۂ�4�ʃT�C�R����U����"A,D�Ƃł�m���h���g����ׂɉ�I�����Đ����ƂȂ�m���h�ɂȂ�A������gA,D�Ƃł�m���h=�g50%�h���������ʂɂȂ�n�Y�ł��̒l�͖����҂̐ݒ肵�������Ɩ������ĂȂ��ł���H�Ƃ����̂����l�^�̃��W�b�N�Ȃ�Ȃ��́H
�A���A�ςȂ��Ə�����
�Ⴄ��
>>952 �L���Ȃ�H
�����͂ǂ��������W�b�N�Ȃ�H
�́A���̂悤�Ȗ����������Ƃ�����B���Ԃ�A�ޑ�B
����ς���Ƃ��Ė���������C�������
>>954 �L�����Ă̂�VIP��Ȃ�J�ɂ��܂ɃX�������Ă��Ă����Ȃ܂Ƃ߃T�C�g�ł܂Ƃ߂��Ă���Ęb��
���m�ȓ������o�Ȃ�����n�����ނ�ăX�����L�т�
>>957 �ȂA�����m���Ă�킯����Ȃ��̂�
�X�}�������̖{�ł͂ǂ��Ȃ��Ă��H
�܂����̉摜���R�������ė������Ă邩�H
�������炾�������c
>>961 �}�W�ŃR���Ȃ�H
�܂������͂Ȃ��Ƃ͎v�����ǃ~���I�l�A�̕����̓����ƃX�}�������̓����͂ǂ��Ȃ��Ă����m�肽�������Ȃ��ǁA�����������̕������̂Ȃ��������Ď��H
�ǂ��\�[�X�H
�Ȃ������؋����o���ƌ����Ă���
�ł����`���N�`�����X���Ă���H
�Ȃ�ق�
�Ƃ��������
�C���A���ɂ����܂ł��ăz���g�ɕ��������������Ȃ����������ׂ�C�ɂ͂Ȃ��w
�ʃX���ɂ��������
���̐����̒�����ӂɂ��O�p�`���l����B���̎��A�ӂ̒����̍��v��100�ɂȂ�悤�Ȃ��̂͂������邩�B
u = b+c-a, v = c+a-b, w = a+b-c�Ƃ�����u+v+w = a+b+c = 100, u �� v �� w �� 0 ( mod 2 ), u,v,w>0��
���A�����Ȃ�_�u���J�E���g���Ă��
u = b+c-a, v = c+a-b, w = a+b-c�Ƃ�����u+v+w = a+b+c = 100, u �� v �� w �� 0 ( mod 2 ), u,v,w>0��
>>975 �Ђ�������Đ����Ă݂���
> head(z)
[,1] [,2] [,3]
[1,] 2 49 49
[2,] 3 48 49
[3,] 4 47 49
[4,] 4 48 48
[5,] 5 46 49
[6,] 5 47 48
> tail(z)
[,1] [,2] [,3]
[203,] 31 33 36
[204,] 31 34 35
[205,] 32 32 36
[206,] 32 33 35
[207,] 32 34 34
[208,] 33 33 34
208��ނƍ��v�B
���p���
�O
>>947 >>997 �o(500+667)/2�p�~(667-500)=1167�~84=98028
�ӎO�p�`251〜333
83�~3=249
98028-249=97779
��97779��
>>977 �Ώ̊܂ލ����Ȃ��̂�1��
a��b��c��a+b=1000-c��2c
334��c��500
a��b��c��a+b��2b
c/2��b��c
c=2n-1
n��b��2n-1
2n-1-n+1=n
c=2n
n��b��2n
2n-n+1=n+1
c=334
n=167
c=335,336
n=168
c=499,500
n=250
167+1+[n=167,250](n+n+1)=168+(250-167+1)(334+1+500+1)/2=168+84�~836/2=168+84�~418=168+35112=35280
�v���O�����ɐ����������炱���Ȃ����B
>>980 >c��a+b=1000-c��2c
c��a+b-1=1000-c-1��2c
333��c��499
>b��c��a+b��2b
b��c��a+b-1��2b-1
(c+1)/2��b��c
c=2n-1
n��b��2n-1
2n-1-n+1=n
c=2n
n+1��b��2n
2n-(n+1)+1=n
c=333,334
n=167
c=497,498
n=249
c=499
n=250
[n=167,249](n+n)+250=(249-167+1)(334+498)/2+250=83�~832/2+250=83�~416+250=34528+250=34778
�Ȃ��n=100�̏ꍇ�ɐ����ʼn����Ă郌�X���Ă����n=1000�ʼn��������K�v������́H
>>982 >c��a+b-1=1000-c-1��2c
c��a+b-1=1000-c-1��2c-1
>333��c��499
334��c��449
167+[n=168,249](n+n)+250=167+(249-168+1)(336+498)/2+250=167+82�~834/2+250=167+82�~417+250=167+34194+250=34611
���p���W���
������߂Ă����
r�𐳂̐��Ƃ���
>>983 �듚�����e����Ă����ˁB
����������̂͗��ẴJ�E���g����B
���ʂ͌��Z���肪�Ƃ��������܂��A�Ɣ�������̂��u�ǐS�v�̂���l�Ԃ��Ɖ��͎v���B
�٘_�͔F�߂�B
���Ɋ��݂����A�듚�𓊍e���Ă���l�ɃA�h�o�C�X�ł���̂��l�\�Ȃ��ˁB
���w���ď������l�|����ԃN�Y�l�Ԃ������Ƃ����̂����̈�ہB
�٘_�͔F�߂�B
>>988 ����Ȃ�
������������
���Ȃ��ɂ��̃t���X���ɏ������ސ����̐��w�͂���܂���
>>987 aₙ(r) = 1^r - 2^r + 3^r - 4^r +...+ (-1)^(n-1) n^r��r�̊��ƌ���
1/2^n)/ (1-2^(1+r))��[k=1,n] C[n,k] a[k] = ��(-r)
�������悢
re(r) << 0 �ł͖��炩�Ȃ̂ō��ӂ�r�ɂ��Ă̐������ɂȂ鎖�������͂悢
����č��ӂ��Ǐ���l�R�[�V�[�ł��鎖�������͂悢
������
1/2^(n+1)a_(n+1)(r)
+(1/2^(n+1))��[k=1,n](C[n,k-1]-C[n,k])a_k(r)
�ő�ꍀ�͖��炩�ɋǏ���l�ɐ�Ύ�������
���O(1/2^(n+1)(C[n,k-1]+C[n,k])n^(r+1))�Ȃ̂�n��k�ő������킹��Ƃ��Ǐ���l�ɐ�Ύ�������
>>989 �듚�����l�ɏ������ł��Ȃ��悤�ȃN�Y�l�Ԃɂ͂Ȃ肽���Ȃ��Ȃ��B����e�J�����ł̌��͌��Z�ɖ𗧂B
���肪�Ƃ��A�ƌ�����̂��ǐS���������l�Ԃ��Ǝv���B
>>991 �������������Ȃ�975�̉̈Ӗ�����킩���ĂȂ����H
�킩���Ă��琔�l�`�����`�����ς��邾���ʼn����Ă��܂�
>>977 �Ȃ�ďo���Ȃ��ł���H
975���x���̉��ǂ߂Ȃ��l�Ԃ͂��̃X���ł͉��ɂ��ł��܂���
>>993 >975���������Ƃ��������́H
>>994 ���Ȃ������Ő��������Ċm�F���Ă���H
������
>>977 �̖��o�����_�ł����̉�@�ŏu�E�ł��Ă��܂����ǂ����m�F�ł�����H
�������Ȃ�
>>999 975�������ł��Ȃ��A�z�̗Ȃǐ�����0
���̃X���b�h�͂P�O�O�O���܂����B
5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/ �� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php
�j���[�X �X�|�[�c �Ȃ�ł� ����
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1640443648/ �q���g�F http ://xxxx.5chb .net/xxxx �̂悤��b �����邾���ł����ŃX���ۑ��A�{���ł��܂��BTOP�� TOP�� �@
�S�f���ꗗ ���̌f���� �l�C�X�� |
>50
>100
>200
>300
>500
>1000��
�V���摜 ���u�ʔ������w�̖�肨�����ā`�� 40��� ->�摜>17�� �v �������l�����Ă��܂��F�E�ʔ������w�̖�肨������~�� 44��� �ʔ������w�̖�肨������~�� 41��� �ʔ�����肨�����ā`�� 34��� �ʔ�����肨�����ā`�� 26��� �ʔ�����肨�����ā`�� 31��� ���]�������w���������Ă��������B(����) �S�Ή�吔�w���W ���w�����߂Ƃ������n�̊w��ƓN�w�ɂ��ā@�W ���w�����߂Ƃ������n�̊w��ƓN�w�ɂ��ā@�P�U �v���X�G���[�g�Ƃ������ŋ��̐��w���W �y��b��W����z���w��萸�u�y20���ځz �y�₳���z1��1�I����̐��w���W�X��5�y�n�C���z ���w���p�́w�VA�N���X���w���W�x1�N�`3�N ���w���W��Έ�Ή������X�� ���w2�N�̐��w�̖������ā` ���w�̖������Ă�Ɣ߂����Ȃ��� ���吔�w�̔��ς̖����ĊȒP��� ���w�̖��Ŏ���ł� ���̐��w�̖�苳���� ���̐��w�̉�@�̖��_�������Ă��� ���w�҂̏������ʔ������� ���w�̖������Ă݂��[�[�[�[ ���w���ł������鐔�w�̖����o���Ă� ���������̍��Z�̐��w�̖������� �����ʼnY������w�̖�茩���� ���w�̖����N���Ăǂ��̑�w�����ĂĂ݂Ă� ���Z���w�̖����o���������������X�� �^��w��������̐��w�̖��̉����� ���w�̖��W�ł悭���錙���ȑ�w�����Ă� ���w�̋Ɍ��̖��ł킩��Ȃ��̂�������� ���̖��A��w�ւ̐��w�ł����Ɖ����x���H �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 60 �y�N��z����������w����A����Ɗm���̖����o��I�I �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 53 �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 54 �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 62 �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 57 �����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 61 �I���ɐ��w�̖�蒮���Ă����������̒j�ƕt�������Ă��� ���̉摜�ɍڂ��Ă鐔�w�̖����đ��̖��W�Ō�������ǂꂭ�炢�̓�Փx�H ��3�k���w���u�]�����ǐ��w�̂������߂̖��W�����ĉ����� ���������w�̖���������������� ���w��Vipper�ǂ��͉�����H�H �y�����z���w�͂���Ȃɖʔ����I�X�@�S�� �㐔���l�̂ɂ���[4��5��] �y1A�z�Z���^�[�����̐��w�ŗ��ō��̗ǖ���āA����ς��̔N�̂��̖�肾��ȁI�I�I�I�y2B�z �y���w�z�u�O�����̒藝�v���ЂƖڂŕ�����W�����ʔ����Ƙb��Ɂ@�u���o�I�ɂ킩��v�u���������̂��w�Z�ɂ�������v �y�T�b�J�[�z�������͂܂��v�t�ɍs����\��������H�������{��|����..�u���w�̖��������Ă݂悤�v�Ƃ��ďo�ꂪ���܂�p�^�[�����l�@ [Egg��] ���w�̖ʔ����b���� (69) �����w���t��ق点�����y�g�����v�̖��z ���̖�肨�����Ă������� �������ɂȂ�ɕK�v�Ȑ��w���������Ă��� ���w���Ďc������� �������w�Ȃ̋������Ȃ���� �Ԃ����Ⴏ������w���͐��w�Q�[����� �O�p��������Ő��w���߂��l������� ���w����Ă����Č��\�u��������Ȃ��v��� ���^�N���n���Ă₽�琔�w�ł���l��_�i�����Ă��� ���w�Ōv�Z�o���Ȃ����Ƃ��Ă���́H��������A�������� ���w�ƕ����Ə��̊w�͂́@�H�ƍ��Z�����������ʉȗ��n�@����� ���ǃZ���^�[�����́u2014�N����v��u2015�N���w2B�v������͌���邱�ƂȂ����������� �Љ�ɏo����킩�邯�ǁu�앶�v��u�Ǐ����z���v�̃X�L�����Ė����ꒃ�𗧂�� ���w��Љ�Ƃ����͂邩�ɖ𗧂� �o�c�A�u�Ȋw�I�H�w�I���w�I�_�C�o�[�V�e�B�I�C���N���[�W�����I�����������点����v�@�@���{�̋��炾�ƕ��n��C�V�X�g��������� �^�J���b�V��(���A����T��)�@10��� teratail���肠����tail�H 22���(��) ���nTwitter�r������� Part10
23:47:09 up 84 days, 45 min, 0 users, load average: 8.61, 9.60, 9.90
in 2.1665091514587 sec
@2.1665091514587@0b7 on 071012