���ɐi�w�Z�ƌĂ��w�Z�̓������́A��ؓ�ł͂����܂���B���ɂ͑�w�����l�ł���킵�Ă��܂��悤�Ȗ����B����́A�S���g�b�v���x���̕��l���ւ鐼�̖���Z�E�咆�w�Z��2018�N�x��������A���j�[�N�Ȗ����`���C�X�B�F����͏��w���ɏ��Ă܂����H

�����̏o��2����@�ɂ��Ă̖��ł��B
10m�̂̂ڂ�_�ɓo��ƁA���̐l��艽�b�������̏o�����邱�Ƃ��o����ł��傤�H
�i����30�N�x �咆�w�Z�������E����-����j
�o��_��o��ƒn��ɂ���l���킸���ɑ������̏o�����邱�Ƃ��ł��܂��B���̌シ���o��_���~���ƁA����1�x���̏o�����邱�Ƃ��ł��A���ʏ����̏o��2�邱�Ƃ��ł��܂��B�܂�A���̖��������ƁA���b�ȓ��ɓo��_����~���Ώ����̏o��2�邱�Ƃ��ł���̂���������̂ł��B
������
�n���͊��S�ȋ��̂Ƃ��A���a6400km�A�~��40000km�Ƃ��Čv�Z���Ă��܂�Ȃ��B
A�n�_��B�n�_�͂Ƃ��ɐԓ���Ƃ���B
h�͏\���ɒZ���̂ŁAAB�̒���=AC�̒����Ƃ��Ă悢�B
�ϑ��҂̐g���͖����ł�����̂Ƃ���B
�Εӂ̒���c�A���̓�ӂ̒���a, b�̒��p�O�p�`�ɂ��āAa�~a+b�~b=c�~c�����藧�i�O�����̒藝�j�B
�����_���ʂ��l�̌ܓ����Đ����œ����邱�ƁB
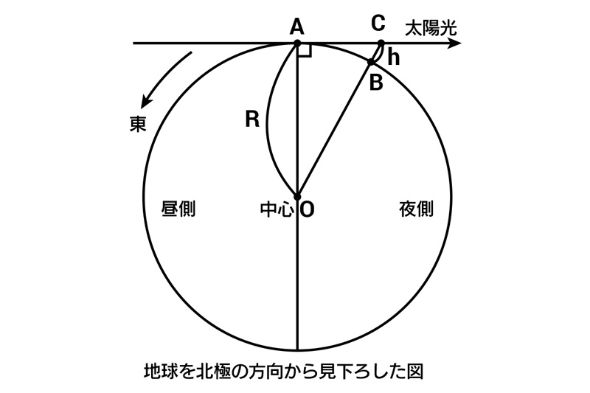
�i����30�N�x�咆�w�Z�����E���ȁ@����j
�����
���������u���̏o������v�Ƃ́A���̐}�́u���z���v�ɐڂ���Ƃ������Ƃ��Ӗ����܂��B�}�ł�A�n�_��C�n�_�œ����ɓ��̏o���}���Ă��܂��BB�n�_�͂��̎��_�ł͖鑤�Ȃ̂ŁA�܂����̏o���}���Ă��܂��A�n���̎��]�ɂ��A�Ԃ��Ȃ����̏o���}���邱�Ƃł��傤�B
���̖��Őu����Ă���̂́AC�n�_�ł�B�n�_��艽�b�������̏o�������邩�B�}�̎��_�ł͂��傤��C�n�_�œ��̏o�����Ă���̂ŁA���̖��́A�uB�n�_�ł����̏o��������̂́A���̐}���牽�b��̂��Ƃ��H�v�ƌ����������܂��B
�܂�AB�n�_���}��A�n�_�ɂ��ǂ蒅���܂ŁA���b������̂��A���v�Z����悢�̂ł��B�n���̎��]�́A24���Ԃ�1�����܂��B����͒n����1����40000km�ƒ�߂��Ă���̂ŁA�n�ʂ�24���Ԃ�40000km�����Ă���ƍl�����܂��B
���ܒm�肽���̂́AB�n�_����A�n�_�܂ł̎��]�͂ǂꂭ�炢������̂��A�Ȃ̂ŁAAB�̒�������������A���Ƃ͌v�Z���邾���ł��ˁBAB=AC�Ƃ��Ă悢�̂ŁA�O�p�`OAC�ɂ��āA�O�����̒藝���g����AC�̒��������߂܂��傤�B10m��0.01km�Ȃ̂ŁA
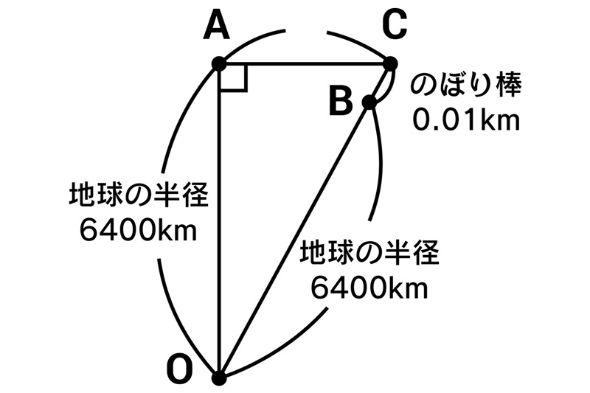
AC��2��=OC��2��-OA��2��
AC^2=�i6400+0.01�j^2-6400^2
AC^2=�i6400^2+6400�~0.01�~2+0.01^2�j-6400^2
AC^2��6400�~0.01�~2
AC^2��128
AC��11.3
�܂�AAB�̒�����11.3km�ƂȂ�܂��B���������͖ڑO�ł��B�n�ʂ�24���ԁi=86400�b�j��40000km�������Ƃ��l����ƁA11.3km�����̂ɂ����鎞�Ԃ́A
11.3���i40000��86400�j��24.4�b
�����_���ʂ��l�̌ܓ�����̂ŁA������24�b�ƂȂ�܂��B����[�A���w���������Ƃ͎v���Ȃ��v�Z�ʂł����B���j�͕������Ă��A�ǂ����Ń~�X���Ă��܂������ł��B
���Ȃ݂ɂ��̖��́A�n��10m�̒n�_����n�ʂ܂�24�b�ȓ��ɍ~���ƁA�n��10m�ň�x���������z���������݁A�n��ł�����x����܂��B����͂��Ȃ킿�u���̕����ɒ���ł������z�v�����邱�Ƃ��ł���A�Ƃ������Ƃ��\���Ă��܂��B
������t�ɂ����A���̓���̒���ɍ����Ƃ���ɓo��ƁA�n��Œ����z����������A�����Ƃ���ł�����x���݂܂��B�����A���Ȃ킿�u�����珸�鑾�z�v�����邱�Ƃ��ł���̂ł��B
�������Ƃ͂����A�����v�Z��ËL�������邾���łȂ��A�ʔ������Nj������ǖ�ł����B�Ƃ͂����A�����������Ă���������͂���ǂ���ł͂Ȃ��ł��傤���ǁc�c�B
2018�N02��22�� 12��00��
�˂Ƃ��
http://nlab.itmedia.co.jp/nl/articles/1802/22/news040.html
