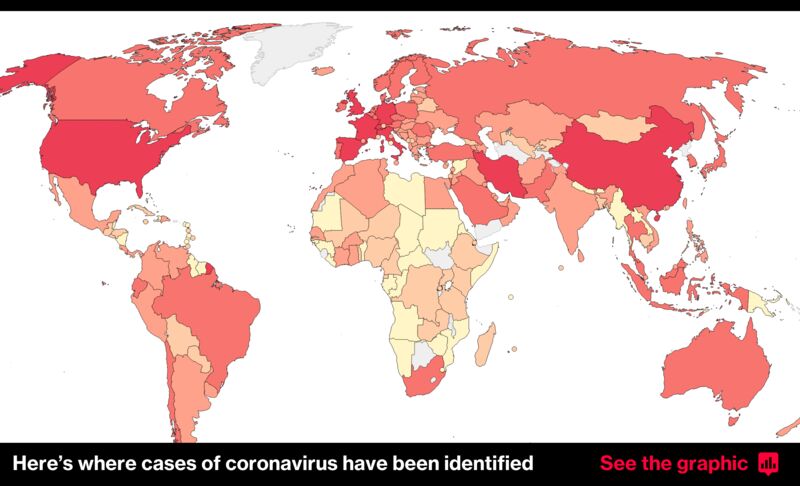
指数関数的に拡散する新型コロナウイルスの対策として、「カーヴの平坦化」こそ重要である数学的な根拠
2020.04.01 WED 12:00、WIRED
■■一部抜粋(後半略)
新型コロナウイルスの感染者数の爆発的増加(いわゆる“オーバーシュート”)を防ぐには、自主隔離などによって早い段階から感染拡大を遅らせることが極めて重要になる。
いわゆる「カーヴの平坦化」と呼ばれる措置だが、なぜこの措置が鍵を握るのか。その根拠を数学的に解説する。
2020.04.01 WED 12:00

新型コロナウイルスによる感染症「COVID-19」が指数関数的に広がっていくことの恐ろしさについては、すでに先日の記事で説明した。
指数関数的な拡大においては、始まってからしばらくは感染者の数はそれほど多くはならない。だが、ある時点から急増する。
これが各国政府が直面している問題だ。最悪の事態を回避するには、事態がそれほどひどくなく、さまざまな緊急措置の必要性が疑問視されるときから対策をとっておく必要がある。
関連記事:新型コロナの感染者数は、かくして指数関数的に「爆発的増加」する
https://wired.jp/2020/03/30/how-fast-does-a-virus-spread/
新型コロナウイルスによる感染症「COVID-19」が指数関数的に広がっていくことの恐ろしさについては、すでに先日の記事で説明した。
指数関数的な拡大においては、始まってからしばらくは感染者の数はそれほど多くはならない。だが、ある時点から急増する。
これが各国政府が直面している問題だ。最悪の事態を回避するには、事態がそれほどひどくなく、さまざまな緊急措置の必要性が疑問視されるときから対策をとっておく必要がある。
関連記事:新型コロナの感染者数は、かくして指数関数的に「爆発的増加」する
感染増加率は低下する
まず、指数関数モデルについておさらいしておこう。スタート時点の感染者数を「N」とすると、2日後となる3日目の感染者数は「2N」になる。
このそれぞれがウイルスを広めていくため、さらに2日後には「4N」になる計算だ。こうして総感染者数は暴走する貨物列車のように増えていく。
次に、以下の数式を思い出して欲しい。感染者数の変化(𝚫N)を時間(𝚫t)で割ると、感染増加率(a)と感染者総数(N)の積に等しくなる。ここでは時間の単位は1日にしておく。

IMAGE BY RHETT ALLAIN
仮に感染者数が1日で20パーセント増える(感染増加率は0.20)と仮定しよう。人口10,000人の小さな町に感染者が1人やってくると(つまり初日の感染者数は1だ)、感染者数の推移は以下のグラフのようになる。
■■ソースの「機能付き画像」をご確認ください
ひと目でその恐ろしさがわかると思う。だが、世界各国の感染状況を調べると、実際にはこうはなっていない。
例えば、今回のパンデミック(世界的大流行)の震源地で感染拡大が始まってから最も時間が経っている中国では、感染者数の推移のグラフは緩やかなS字カーヴに近い形を描いている。
本格的な拡大が始まってから10日間ほどは指数関数的な拡大が続いたが、その後は伸びが緩やかになり、最終的には新規感染者はほぼゼロに近づいた。つまり、悪化の一途をたどったわけではないのだ。

上記のグラフを作成したのは3月半ばころだが、その後も状況は変わっていない。中国の感染件数は全体で80,000件強で横ばいのままだ。ここから何が言えるだろうか。
まず、政府は感染者の隔離、出入国制限、学校やレストランの閉鎖など、さまざまな措置をとった。感染が最初に始まった武漢市および湖北省は封鎖されたため、感染の大きな危険に晒された人々は実質的に中国の総人口14億人の一部だった。
一方、数学的には別の説明もできる。指数関数モデルでは、1日の新規感染者数は無限に増え続ける。
だが、人口が無限でない限りそんなことは起こらない。患者が増えればそれだけ健康な人の数は減っていき、新規の感染者数は落ち込むからだ。
■■以下略、続きはソースをご覧ください。
TEXT BY RHETT ALLAIN
TRANSLATION BY CHIHIRO OKA
日本語
https://wired.jp/2020/04/01/the-promising-math-behind-flattening-the-curve/
WIRED(US)
https://www.wired.com/story/the-promising-math-behind-flattening-the-curve/
WIRED
https://wired.jp/
2020.04.01 WED 12:00、WIRED
■■一部抜粋(後半略)
新型コロナウイルスの感染者数の爆発的増加(いわゆる“オーバーシュート”)を防ぐには、自主隔離などによって早い段階から感染拡大を遅らせることが極めて重要になる。
いわゆる「カーヴの平坦化」と呼ばれる措置だが、なぜこの措置が鍵を握るのか。その根拠を数学的に解説する。
2020.04.01 WED 12:00

新型コロナウイルスによる感染症「COVID-19」が指数関数的に広がっていくことの恐ろしさについては、すでに先日の記事で説明した。
指数関数的な拡大においては、始まってからしばらくは感染者の数はそれほど多くはならない。だが、ある時点から急増する。
これが各国政府が直面している問題だ。最悪の事態を回避するには、事態がそれほどひどくなく、さまざまな緊急措置の必要性が疑問視されるときから対策をとっておく必要がある。
関連記事:新型コロナの感染者数は、かくして指数関数的に「爆発的増加」する
https://wired.jp/2020/03/30/how-fast-does-a-virus-spread/
新型コロナウイルスによる感染症「COVID-19」が指数関数的に広がっていくことの恐ろしさについては、すでに先日の記事で説明した。
指数関数的な拡大においては、始まってからしばらくは感染者の数はそれほど多くはならない。だが、ある時点から急増する。
これが各国政府が直面している問題だ。最悪の事態を回避するには、事態がそれほどひどくなく、さまざまな緊急措置の必要性が疑問視されるときから対策をとっておく必要がある。
関連記事:新型コロナの感染者数は、かくして指数関数的に「爆発的増加」する
感染増加率は低下する
まず、指数関数モデルについておさらいしておこう。スタート時点の感染者数を「N」とすると、2日後となる3日目の感染者数は「2N」になる。
このそれぞれがウイルスを広めていくため、さらに2日後には「4N」になる計算だ。こうして総感染者数は暴走する貨物列車のように増えていく。
次に、以下の数式を思い出して欲しい。感染者数の変化(𝚫N)を時間(𝚫t)で割ると、感染増加率(a)と感染者総数(N)の積に等しくなる。ここでは時間の単位は1日にしておく。

IMAGE BY RHETT ALLAIN
仮に感染者数が1日で20パーセント増える(感染増加率は0.20)と仮定しよう。人口10,000人の小さな町に感染者が1人やってくると(つまり初日の感染者数は1だ)、感染者数の推移は以下のグラフのようになる。
■■ソースの「機能付き画像」をご確認ください
ひと目でその恐ろしさがわかると思う。だが、世界各国の感染状況を調べると、実際にはこうはなっていない。
例えば、今回のパンデミック(世界的大流行)の震源地で感染拡大が始まってから最も時間が経っている中国では、感染者数の推移のグラフは緩やかなS字カーヴに近い形を描いている。
本格的な拡大が始まってから10日間ほどは指数関数的な拡大が続いたが、その後は伸びが緩やかになり、最終的には新規感染者はほぼゼロに近づいた。つまり、悪化の一途をたどったわけではないのだ。

上記のグラフを作成したのは3月半ばころだが、その後も状況は変わっていない。中国の感染件数は全体で80,000件強で横ばいのままだ。ここから何が言えるだろうか。
まず、政府は感染者の隔離、出入国制限、学校やレストランの閉鎖など、さまざまな措置をとった。感染が最初に始まった武漢市および湖北省は封鎖されたため、感染の大きな危険に晒された人々は実質的に中国の総人口14億人の一部だった。
一方、数学的には別の説明もできる。指数関数モデルでは、1日の新規感染者数は無限に増え続ける。
だが、人口が無限でない限りそんなことは起こらない。患者が増えればそれだけ健康な人の数は減っていき、新規の感染者数は落ち込むからだ。
■■以下略、続きはソースをご覧ください。
TEXT BY RHETT ALLAIN
TRANSLATION BY CHIHIRO OKA
日本語
https://wired.jp/2020/04/01/the-promising-math-behind-flattening-the-curve/
WIRED(US)
https://www.wired.com/story/the-promising-math-behind-flattening-the-curve/
WIRED
https://wired.jp/